Слушайте и смотрите новую подборку лекций Техносферы Mail.Ru. На этот раз представляем в открытом доступе весенний курс «Введение в анализ данных», на котором слушателей знакомят со сферой анализа данных, основными инструментами, задачами и методами, с которыми сталкивается любой исследователь данных в работе. Курс преподают Евгений Завьялов (аналитик проекта Поиск Mail.Ru, занимающийся извлечением полезных бизнесу знаний из данных, генерируемых поисковым движком и десктопными приложениями), Михаил Гришин (программист-исследователь из отдела анализа данных) и Сергей Рыбалкин (старший программист из студии Allods Team).

Лекция 1. Введение в Python

Из первой лекции вы узнаете, что такое анализ данных, какие инструменты используют для анализа данных, а также как работает Python.

Некоторое время назад в московский офис Яндекса приезжал Игорь Пак — ученый с множеством научных работ, выпускник мехмата МГУ и аспирантуры Гарварда. Сейчас Игорь работает в Калифорнийском университете. Его лекция в Яндексе была посвящена различным классам последовательностей и перестановкам. В том числе прямо по ходу лекции он представил выкладки, опровергающие гипотезу Нунана и Зайлбергера — одну из ключевых в области перестановок.



Под катом — подробная текстовая расшифровка и большинство слайдов.

Занимаясь музыкальным творчеством, я часто делаю аранжировки и записи на компьютере — используя кучу всяких VST плагинов и инструментов. Стыдно признаться — я никогда не понимал, как "накручивают" звуки в синтезаторах. Программирование позволило мне написать свой синтезатор, "пропустить через себя" процесс создания звука.

Я планирую несколько статей, в которых будет пошагово рассказано, как написать свой VST плагин/инструмент: программирование осциллятора, частотного фильтра, различных эффектов и модуляции параметров. Упор будет сделан на практику, объяснение программисту простым языком, как же все это работает. Теорию (суровые выводы и доказательства) обойдем стороной (естественно, будут ссылки на статьи и книги).

Обычно плагины пишутся на C++ (кроссплатформенность, возможность эффективно реализовать алгоритмы), но я решил выбрать более подходящий для меня язык — C#; сфокусироваться на изучении самого синтезатора, алгоритмов, а не технических деталей программирования. Для создания красивого интерфейса я использовал WPF. Возможность использования архитектуры .NET дала возможность библиотека-обертка VST. NET.

Ниже представлен обзорный ролик моего простого синтезатора, полученных интересных звучаний.

Предстоит нелегкий путь, если вы готовы — добро пожаловать под кат.

Фильмы, где огромные армии сходятся друг с другом на поле боя в эпичной битве обычно вызывают в людях бурю эмоций. Сцены сражений из "Звездных войн" с мастерски владеющими световыми мечами джедаями и ордами боевых дроидов — не исключение.

Но иногда бывает интересно посмотреть на сам процесс битвы как бы с высоты птичьего полета и увидеть весь ход развития событий. Для этого можно использовать различные средства виртуальной симуляции. В этом посте приведен пример моделирования битвы между боевыми дроидами Федерации и орденом Джедаев с помощью такой простой дискретной модели как клеточный автомат.

В течение последних шести лет в Яндексе идет работа над системой под кодовым называнием YT (по-русски мы называем её «Ыть»). Это основная платформа для хранения и обработки больших объемов данных — мы уже о ней рассказывали на YaC 2013. С тех пор она продолжала развиваться. Сегодня я расскажу о том, с чего началась разработка YT, что нового в ней появилось и что ещё мы планируем сделать в ближайшее время.



Кстати, 15 октября в офисе Яндекса мы расскажем не только о YT, но и о других наших инфраструктурных технологиях: Media Storage, Yandex Query Language и ClickHouse. На встрече мы раскроем тайну — расскажем, сколько же в Яндексе MapReduce-систем.

Какую задачу мы решаем?

По роду своей деятельности Яндекс постоянно сталкивается с необходимостью хранить и обрабатывать данные таких объемов, с которыми обычному пользователю никогда не приходится иметь дело. Поисковые логи и индексы, пользовательские данные, картографическая информация, промежуточные данные и результаты алгоритмов машинного обучения — все это может занимать сотни петабайт дискового пространства. Для эффективной обработки подобных объемов традиционно используется парадигма MapReduce, позволяющая достичь хорошего баланса между эффективностью вычислений и простотой пользовательского кода.

James Kyle как-то раз взял и написал пост про структуры данных, добавив их реализацию на JavaScript. А я взял и перевёл.

Дисклеймер: в посте много ascii-графики. Не стоит его читать с мобильного устройства — вас разочарует форматирование текста.

На написание данного поста меня подвигла недавняя публикация этого и вот этого переводов, в которых авторы в интеллигентной форме выражают свое недовольство по поводу того, как O-оценки вычислительной сложности классических, казалось бы, алгоритмов вступили в диссонанс с их практическим опытом разработки. Основным предметом критики послужила модель памяти, в рамках которой эти оценки были получены — она, де, не учитывает особенности иерархической организации по принципу быстродействия, которая имеет место быть в современных вычислительных системах. От чего и произрастают все последующие неприятности. И судя по наблюдаемой реакции благодарных читателей, авторы далеко не одиноки в своем негодовании и желании «наехать» на классиков с их О-большими. Так возможно, действительно стоит отправить на свалку истории выкладки дядек в белых халатах, сделанные ими для ламповых тугодумающих и пышащих жаром машин, и дать дорогу молодым амбициозным моделям, более точно отражающим анатомию современного «железа»?


Давайте разбираться

Городская библиотека Стокгольма. Фото minotauria.

В этой статье я хочу рассказать о том, что оценивать время обращения к памяти как O(1) — это очень плохая идея, и вместо этого мы должны использовать O(√N). Вначале мы рассмотрим практическую сторону вопроса, потом математическую, на основе теоретической физики, а потом рассмотрим последствия и выводы.

Введение

Если вы изучали информатику и анализ алгоритмической сложности, то знаете, что проход по связному списку это O(N), двоичный поиск это O(log(N)), а поиск элемента в хеш-таблице это O(1). Что, если я скажу вам, что все это неправда? Что, если проход по связному списку на самом деле O(N√N), а поиск в хеш-таблице это O(√N)?

Не верите? Я вас сейчас буду убеждать. Я покажу, что доступ к памяти это не O(1), а O(√N). Этот результат справедлив и в теории, и на практике. Давайте начнем с практики.

Измеряем

Давайте сначала определимся с определениями. Нотация “О” большое применима ко многим вещам, от использования памяти до запущенных инструкций. В рамках этой статьи мы O(f(N)) будет означать, что f(N) — это верхняя граница (худший случай) по времени, которое необходимо для получения доступа к N байтов памяти (или, соответственно, N одинаковых по размеру элементов). Я использую Big O для анализа времени, но не операций, и это важно. Мы увидим, что центральный процессор подолгу ждет медленную память. Лично меня не волнует, что делает процессор пока ждет. Меня волнует лишь время, как долго выполняется та или иная задача, поэтому я ограничиваюсь определением выше.

Добро пожаловать во вторую часть серии статей о физике судов в видеоиграх. В первой части я объяснял принципы выталкивания и обосновал выбор расчёта гидростатических сил, действующих на судно. Также я указал, что мы закладываем важный фундамент для расчёта не только гидростатических сил, но и для гидродинамических сил в нашей упрощённой модели. Я имею в виду, что мы рассчитаем дополнительные силы для каждого погружённого треугольника, суммируем их и приложим их к судну. Всё действительно будет настолько просто.

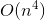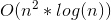Доброго всем времени суток, уважаемые посетители сайта Хабрахабр. В данной статье я бы хотел рассказать вам о том, что такое диаграмма Вороного (изображена на картинке ниже), о различных алгоритмах её построения (за , — пересечение полуплоскостей, 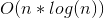— алгоритм Форчуна) и некоторых тонкостях реализации (на языке C++).



Также будет рассмотрено много интересных применений диаграммы и несколько любопытных фактов о ней. Будет интересно!

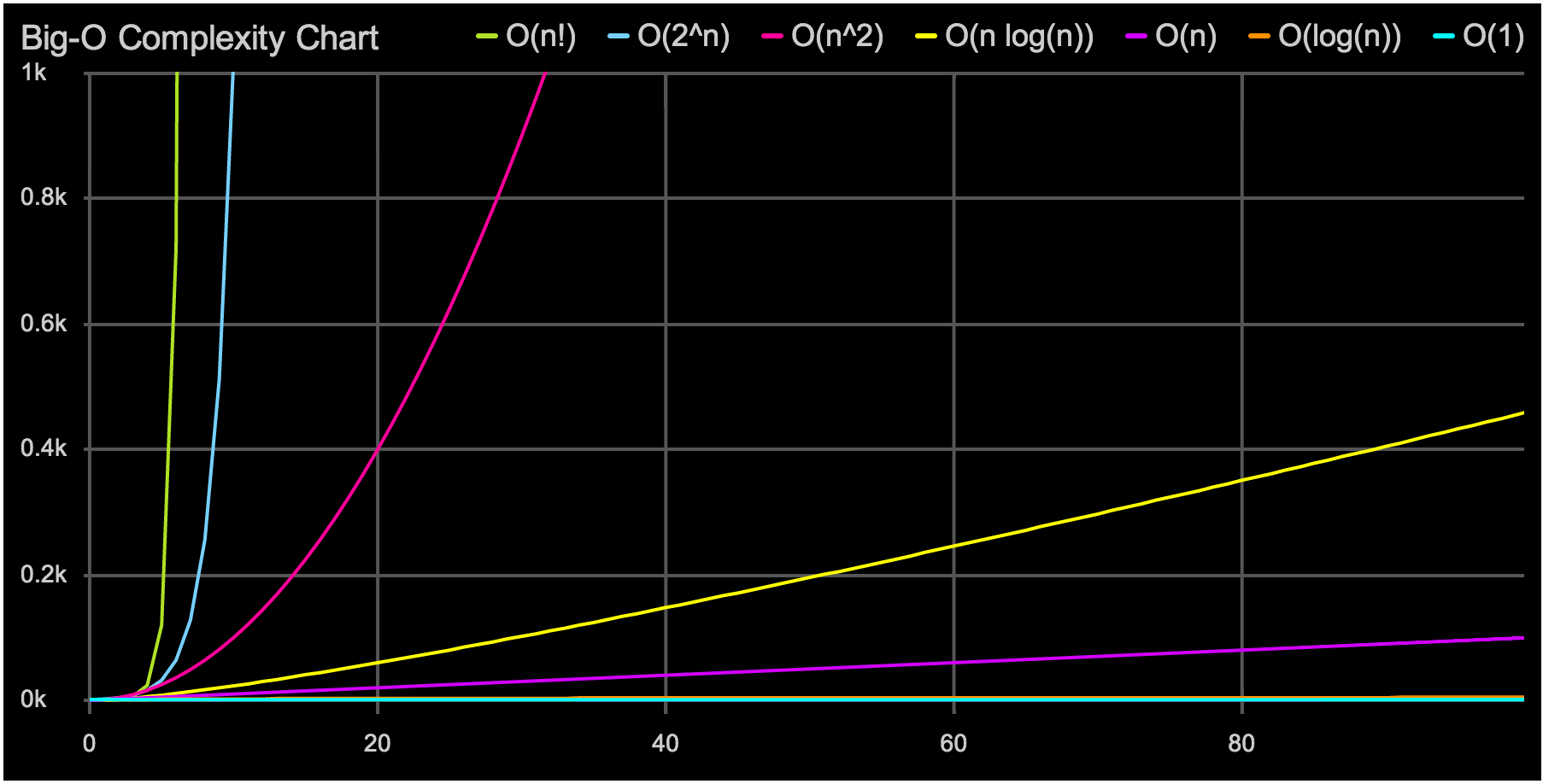
"О" большое — это отличный инструмент. Он позволяет быстро выбрать подходящую структуру данных или алгоритм. Но иногда простой анализ "О" большого может обмануть нас, если не подумать хорошенько о влиянии константных множителей. Пример, который часто встречается при программировании на современных процессорах, связан с выбором структуры данных: массив, список или дерево.

Память, медленная-медленная память

В начале 1980-х время, необходимое для получения данных из ОЗУ и время, необходимое для произведения вычислений с этими данными, были примерно одинаковым. Можно было использовать алгоритм, который случайно двигался по динамической памяти, собирая и обрабатывая данные. С тех пор процессоры стали производить вычисления в разы быстрее, от 100 до 1000 раз, чем получать данные из ОЗУ. Это значит, что пока процессор ждет данных из памяти, он простаивает сотни циклов, ничего не делая. Конечно, это было бы совсем глупо, поэтому современные процессоры содержат несколько уровней встроенного кэша. Каждый раз когда вы запрашиваете один фрагмент данных из памяти, дополнительные прилегающие фрагменты памяти будут записаны в кэш процессора. В итоге, при последовательном проходе по памяти можно получать к ней доступ почти настолько же быстро, насколько процессор может обрабатывать информацию, потому что куски памяти будут постоянно записываться в кэш L1. Если же двигаться по случайным адресам памяти, то зачастую кэш использовать не получится, и производительность может сильно пострадать. Если хотите узнать больше, то доклад Майка Актона на CppCon — это отличная отправная точка (и отлично проведенное время).

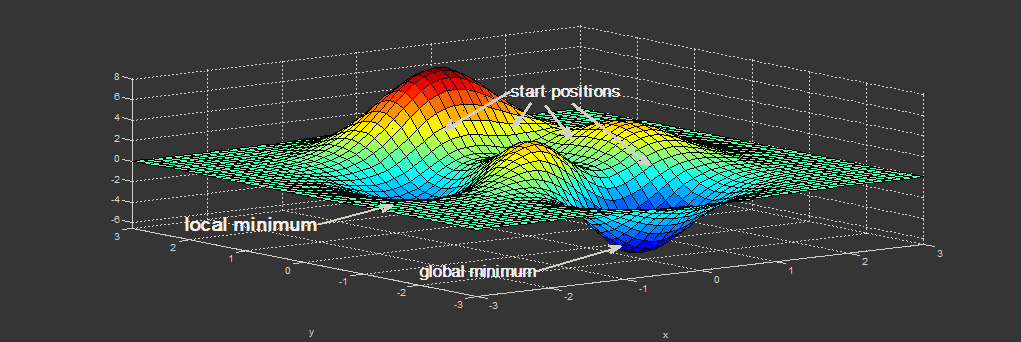
Нахождение экстремума(минимума или максимума) целевой функции является важной задачей в математике и её приложениях(в частности, в машинном обучении есть задача curve-fitting). Наверняка каждый слышал о методе наискорейшего спуска (МНС) и методе Ньютона (МН). К сожалению, эти методы имеют ряд существенных недостатков, в частности — метод наискорейшего спуска может очень долго сходиться в конце оптимизации, а метод Ньютона требует вычисления вторых производных, для чего требуется очень много вычислений.

Для устранения недостатков, как это часто бывает, нужно глубже погрузиться в предметную область и добавить ограничения на входные данные. В частности: МНС и МН имеют дело с произвольными функциями. В статистике и машинном обучении часто приходится иметь дело с методом наименьших квадратов (МНК). Этот метод минимизирует сумму квадрата ошибок, т.е. целевая функция представляется в виде

Алгоритм Левенберга — Марквардта является нелинейным методом наименьших квадратов. Статья содержит:

• объяснение алгоритма
• объяснение методов: наискорейшего спуска, Ньтона, Гаусса-Ньютона
• приведена реализация на Python с исходниками на github
• сравнение методов

В приложении 2ГИС теперь есть навигатор. Мы научились «ехать» по треку, озвучивать манёвры, автоматически перестраивать маршрут, рассчитывать время в пути, доводить пользователя до входа в здание или организацию, учитывая заборы и шлагбаумы, — и всё это в честном офлайне. Пробки (вот разве что для них нужен интернет), разведённые мосты и перекрытые улицы учитываем давно. Пока в нашем навигаторе — необходимый минимум. Чуть позже научим его предупреждать о слишком высокой скорости, лежачих полицейских и камерах ГИБДД, настроим ночной режим, сделаем маршруты по платным и грунтовым дорогам опциональными. Чтобы воспользоваться им, нужно обновить 2ГИС в своем смартфоне или скачать в AppStore или Windows Store. Для Android обновление выходит постепенно, начиная с 22 августа (будет доступно на всю аудиторию к сентябрю).

А сегодня расскажем, как навигатор 2ГИС предугадывает положение автомобиля и плавно перемещает стрелочку по маршруту. Ведь именно качество ведения пользователя по маршруту определяет эргономику интерфейса любого современного навигатора, простоту ориентирования на местности и своевременность совершения манёвров.

Одна из основных функций десктопного клиента Облака Mail.Ru — синхронизация данных. Ее целью является приведение папки на ПК и ее представления в Облаке к одинаковому состоянию. При разработке этого механизма мы встретились с некоторыми, с первого взгляда, достаточно очевидными особенностями различных файловых и операционных систем. Однако если о них не знать, можно столкнуться с довольно неприятными последствиями (не получится загрузить или удалить файл). В этой статье мы собрали особенности, знание которых позволит вам правильно работать с данными на дисках и, возможно, убережет от необходимости срочного хотфикса.

Приветствую тебя, Хабр! Наверняка вы заметили, что тема стилизации фотографий под различные художественные стили активно обсуждается в этих ваших интернетах. Читая все эти популярные статьи, вы можете подумать, что под капотом этих приложений творится магия, и нейронная сеть действительно фантазирует и перерисовывает изображение с нуля. Так уж получилось, что наша команда столкнулась с подобной задачей: в рамках внутрикорпоративного хакатона мы сделали стилизацию видео, т.к. приложение для фоточек уже было. В этом посте мы с вами разберемся, как это сеть "перерисовывает" изображения, и разберем статьи, благодаря которым это стало возможно. Рекомендую ознакомиться с прошлым постом перед прочтением этого материала и вообще с основами сверточных нейронных сетей. Вас ждет немного формул, немного кода (примеры я буду приводить на Theano и Lasagne), а также много картинок. Этот пост построен в хронологическом порядке появления статей и, соответственно, самих идей. Иногда я буду его разбавлять нашим недавним опытом. Вот вам мальчик из ада для привлечения внимания.

Давайте поговорим о физике транспортных средств

Физика транспортных средств в видеоиграх не очень сильно обсуждается. Статьи в Интернете о физике транспорта в видеоиграх немногочисленны и поверхностны; обычно они посвящены самым основам. Программист транспорта для видеоигр ощущает себя сегодня в относительном вакууме. Возможно, такая ситуация возникла, потому что эту тему довольно сложно объяснить, а может быть, мы просто стыдимся признаваться в использовании хаков, упрощений и хитростей, которые мы вносим по сравнению с «правильной», реалистичной симуляцией физики. Как бы ни обстояло дело, видеоигры имеют уникальные проблемы в симуляции транспорта, а значит, об этом стоит писать. Это захватывающая тема, относящаяся к физике, работе с камерой, звуку, спецэффектам, а также к восприятию и психологии человека.

Я решил сначала поговорить о судах, потому что недавно работал с ними; ещё я обнаружил, что их динамика не совсем понимается даже на уровне исследований (хотя многое и понятно). Модели и теории формулируются таким образом, что их становится сложно применить непосредственно в видеоиграх. Или же они требуют очень ресурсоёмких методов симуляции, которые практически невозможно контролировать и адаптировать под причудливые потребности разработчиков и игроков. Но можно написать упрощённую модель, которая учитывает важные параметры судна. В этом определённо есть доля искусства, «прыжка веры» и небольшая доля «творческой» физики, которая заставит Кельвина и Стокса перевернуться в могилах.

Алиасинг представляет одну из фундаментальных проблем компьютерной графики, и для борьбы с ним придумано множество разнообразных алгоритмов антиалиасинга. Появление MLAA привлекло интерес к алгоритмам, работающим на этапе постобработки. Одним из таких алгоритмов (с небольшой оговоркой) является Geometry Buffer Anti-Aliasing (GBAA). В этом материале описана попытка модификации оригинального алгоритма для улучшения качества антиалиасинга в некоторых случаях.

Kaggle — это платформа для проведения конкурсов по машинному обучению. На Хабре частенько пишут про неё: 1, 2, 3, 4, и.т.д. Конкурсы на Kaggle интересные и практичные. Первые места обычно сопровождаются неплохими призовыми (топовые конкурсы — более 100к долларов). В последнее время на Kaggle предлагали распознавать:

• Диабет по сетчатке глаза
• Фотографии со спутников и их порядок
• Одинаковые рекламные объявления

И многое-многое другое.

Мне давно хотелось попробовать, но что-то всё время мешало. Я разрабатывал много систем, связанных с обработкой изображений: тематика близка. Навыки более лежат в практической части и классических Computer Vision (CV) алгоритмах, чем в современных Machine Learning техниках, так что было интересно оценить свои знания на мировом уровне плюс подтянуть понимание свёрточных сетей.

И вот внезапно всё сложилось. Выпало пару недель не очень напряжённого графика. На kaggle проходил интересный конкурс по близкой тематике.Я обновил себе комп. А самое главное — подбил vasyutka и Nikkolo на то, чтобы составить компанию.

Сразу скажу, что феерических результатов мы не достигли. Но 18 место из 1.5 тысяч участников я считаю неплохим. А учитывая, что это наш первый опыт участия в kaggle, что из 3х месяц конкурса мы участвовали лишь 2.5 недели, что все результаты получены на одной единственной видеокарте — мне кажется, что мы хорошо выступили.

О чём будет эта статья? Во-первых, про саму задачу и наш метод её решения. Во-вторых, про процесс решения CV задач. Я писал достаточно много статей на хабре о машинном зрении(1,2,3), но писанину и теорию всегда лучше подкреплять примером. А писать статьи по какой-то коммерческой задаче по очевидным причинам нельзя. Теперь наконец расскажу про процесс. Тем более что тут он самый обычный, хорошо иллюстрирующий как задачи решаются. В-третьих, статья про то, что идёт после решения идеализированной задаче в вакууме: что будет когда задача столкнётся с реальностью.

Кажется, не проходит и дня, чтобы на Хабре не появлялись посты о нейронных сетях. Они сделали машинное обучение доступным не только большим компаниям, но и любому человеку, который умеет программировать. Несмотря на то, что всем кажется, будто о нейросетях уже всем все известно, мы решили поделиться обзорной лекцией, прочитанной в рамках Малого ШАДа, рассчитанного на старшеклассников с сильной математической подготовкой.

Материал, рассказанный нашим коллегой Константином Лахманом, обобщает историю развития нейросетей, их основные особенности и принципиальные отличия от других моделей, применяемых в машинном обучении. Также речь пойдёт о конкретных примерах применения нейросетевых технологий и их ближайших перспективах. Лекция будет полезна тем, кому хочется систематизировать у себя в голове все самые важные современные знания о нейронных сетях.



Константин klakhman Лахман закончил МИФИ, работал исследователем в отделе нейронаук НИЦ «Курчатовский институт». В Яндексе занимается нейросетевыми технологиями, используемыми в компьютерном зрении.

Под катом — подробная расшифровка со слайдами.

Введение.

На той неделе darkk описал свой подход к проблеме распознавания состояния моста(сведён/разведён).

Алгоритм, описанный в статье, использовал методы компьютерного зрения для извлечения признаков из картинок и скармливал их логистической регрессии для получения оценки вероятности того, что мост сведён.

В комментариях я попросил выложить картинки, чтобы можно было и самому поиграться. darkk на просьбу откликнулся, за что ему большое спасибо.

В последние несколько лет сильную популярность обрели нейронные сети, как алгоритм, который умудряется в автоматическом режиме извлекать признаки из данных и обрабатывать их, причём делается это настолько просто с точки зрения того, кто пишет код и достигается такая высокая точность, что во многих задачах (~5% от всех задач в машинном обучении) они рвут конкурентов на британский флаг с таким отрывом, что другие алгоритмы уже даже и не рассматриваются. Одно из этих успешных для нейронных сетей направлений — работа с изображениями. После убедительной победы свёрточных нейронных сетей на соревновании ImageNet в 2012 году публика в академических и не очень кругах возбудилась настолько, что научные результаты, а также програмные продукты в этом направлении появляются чуть ли не каждый день. И, как результат, использовать нейронные сети во многих случаях стало очень просто и они превратились из "модно и молодёжно" в обыкновенный инструмент, которым пользуются специалисты по машинному обучению, да и просто все желающие.