Comments 227
по моим ощущениям 99% разработчиков считают, что в условии ON должен быть id из одной таблицы и id из второй.
Потому что так оно и будет в 99% случаев использования (плюс возможно условия на поля, которые можно вынести в where).
Как впрочем и с дублированием строк. Очень редко нужны такие запросы, когда соединение проходит не по уникальному ключу.
Опередили ) как раз хотел написать, что приличные люди джойнят по ключу, по возможности ) хотя, безусловно, бывает всякое.
Однако, к примеру join по пересечению диапазонов ip адресов в моей практике встречался очень часто. Так то зависит от специфики проекта.
В любом случае, надо знать возможности, а применять только там и где надо.
Прямо прочитали мои мысли :)
Я так устал от этих ответов с пересечениями множеств и кругов, что даже перестал поправлять людей
Вместо того, чтобы молча записывать человека в "неумехи", лучше задать наводящий вопрос.
Мол, что будет в случае с дубликатами?
И тогда уже делать выводы.
А откуда дубликаты id в обоих таблицах?
Просто id — это неправильное название в данном случае.
Сбивает с толку.
Считайте, там просто колонка с числами.
Разве кто-то уточнял, что идентификатор должен быть уникальным?
Из википедии
Identifier, a symbol which uniquely identifies an object or record
Я понимаю, что по названию колонки нельзя судить о ее уникальности, но если у человека спросить, сколько будет 2+2, то 4 — это нормальный ответ, хотя в других системах счисления может получиться 11 и 10.
но кто сказал, что это ID записи в таблице?
В этом вся соль. Раз про это ничего не известно, то, как и в случае с 2+2=4, делается допущение, потому что обычно
ID чего угодно
называют ChevoUgodnoId.
В целом моя мысль в том, что если автор дает задачу неформальным, допускающим двоякую трактовку методом, то и ответ может быть не таким, как он ожидал. И ругать тут некого.
Всё зависит от того с какими данными вы работаете и по какому направлению.
В случае аналитики таких запросов почти нет (и ключи бывают выключены :) )
JOIN cities_ip_ranges AS c ON c.ip_range && s.ip
Я, конечно, посмотрел по ссылочке но всё равно не понял прикола. Мне казалось, что "&&" — это обычный алиас на AND, а значит, перефразируя на русский ON условие звучит так: «где c.ip_range кастуется в true И s.ip кастуется в true», т.е. что-то вроде такого:
... ON CAST(c.ip_range AS BOOLEAN) AND CAST(s.ip AS BOOLEAN)
А дальше моя логическая цепочка привела в тупик, так что решил всё же спросить.
В postgresql можно делать свои расширения. По сути, расширение — это набор инструкций, определяющих новые типы данных и операторы для работы со значениями типов
В данном случае в расширении ip4r определены типы ip4 и ip4r, т.е. ip адрес и диапазон ip адресов. А также оператор &&, который для этих типов определен как "пересечение". То есть, если диапазоны пересекаются, то результат операции будет true
В данном случае && не имеет отношения к and
Завтра запилю более подробный пример, щас с телефона неудобно
Мне казалось, что "&&" — это обычный алиас на AND
Этого нет в стандарте. Поэтому поведение необходимо уточнять для каждой СУБД. Где-то это будет алиас для AND, где-то вообще не будет. В postgresql — оператор строго зависит от типов данных операндов. Есть create operator и можете сами на некоторую последовательность символов приклеить любую логику, в том числе можно даже переопределить штатные операторы (операторы ищутся тоже в порядке search_path если не указаны через pg_operator синтаксис).
Например, в чистом postgresql 11 есть 8 разных операторов &&, для разных типов данных операндов.
Во-первых, таблица — это вообще не множество.
Во первых, множество.
По математическому определению, во множестве все элементы уникальны, не повторяются
Кто вам сказал такую глупость? Множество — это просто совокупность элементов. КАКИХ — зависит от того, что вам надо. В первом приближении всё можно считать множествами.
а в таблицах в общем случае это вообще-то не так. Вторая беда, что термин «пересечение» только путает.
Во вторых, есть такая штука — реляционная алгебра. И пересечение двух отношений в терминах реляционной алгебры, это и есть inner join. Да, это не про голые множества: отношение — это множество с особыми свойствами, пересечение — вводится именно для отношений, а не как операция над множествами. Но выглядит это не более чем придиркой.
t1 CROSS JOIN t2 WHERE condition
можно еще короче: t1, t2 where condition
Также, похоже, нужно избегать термина «пересечение».
Не стоит избегать термина пересечение. Если уж докапываться до терминологии, то следует уточнять, что речь не про множества, а про отношения и реляционную алгебру.
Диаграммы Венна — просто наглядны. Да, не точно, но не смертельно. Не вижу, чем их можно заменить, не теряя наглядности.
Кто вам сказал такую глупость? Множество — это просто совокупность элементов. КАКИХ — зависит от того, что вам надо. В первом приближении всё можно считать множествами.
Ну если разбираться глубже, а не поверхностно, то совокупность всё-таки уникальных элементов. Например, вот определение — economic_mathematics.academic.ru/2630/%D0%9C%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2%D0%BE
Могу ещё ссылок накидать.
Ну если разбираться глубже, а не поверхностно, то совокупность всё-таки уникальных элементов
Все дело в том, что считать уникальным. Если вы можете различить единицы, то, например {1, 1, 1, 1, 1} — спокойно может быть множеством. Все что вам нужно — это уметь различать эти единички. Например, по индексу. Вся математика — это по сути надстройка над теорией множеств. Всё есть множества.
Вы не путайте, что относится к самой математике, а что — к ее применению. В определении множества есть требование к различимости элементов. Но нет требования к равенству. Накладываю на множества дополнительное свойство: упорядоченность. И спокойно так различаю одинаковые, на первый взгляд, элементы.
Ок, дайте тогда определение матрицы, например. Вас сильно смущает, к примеру нулевая матрица? Там одни нули. Но вы их можете различить.Вы хотите сказать что вы лично различаете например значение ноль элемента (1,1) и ноль в элементе (2,2) матрицы?
struct {
long val;
uint x;
uint y;
} mat_el_tот которого «на бумагу» выведен только val, то таки да, каждый из этих mat_el_t элементов будет уникальным.
Или, например, можно это представить как матрицу
A = [ x11 x12 x13; x21 x22 x23; x31 x32 x33 ] где x11 = x12 = x13 = x21 = x22 = x23 = x31 = x32 = x33 = 0;
Если мы возьмем нулевую матрицу 3х3, то множество значений val будет V={0}, множество элементов mat_el_t, определяющих эту матрицу будет A={x11, x12, x13, x21, x22, x23, x31, x32, x33}.
Добавив ещё один ноль в множество V={0} никто не получит какое-то иное множество, оно останется таким же = {0}. Точно также, добавив ещё один элемент х11 в множество A, даже если начать теперь всегда скрупулёзно выписывать, что A={x11, x11, x12, x13, x21, x22, x23, x31, x32, x33}, никто не получит множество, определяющее какую-то другую матрицу чем та, что определялась до этого.
Ок, дайте тогда определение матрицы, например. Вас сильно смущает, к примеру нулевая матрица? Там одни нули. Но вы их можете различить.Если теперь в множестве A={x11, x11, x12, x13, x21, x22, x23, x31, x32, x33} начать различать один x11 от другого, то мы получим что на самом деле в множество был добавлен элемент, который отличается от всех остальных элементов, которые были в нём до этого, т.е. что был добавлен не x11, что противоречит изначальному действию.
Вы не путайте, что относится к самой математике, а что — к ее применению. В определении множества есть требование к различимости элементов. Но нет требования к равенству. Накладываю на множества дополнительное свойство: упорядоченность. И спокойно так различаю одинаковые, на первый взгляд, элементы.
значит, в вашей нотации вы потеряли информацию, которую вы используете для различения.
Позвольте, но ведь последовательность записи (положение в списке) — это информация, и она никуда не терялась.
Кортеж — это упорядоченный набор элементов.
Я попробую внести ясность во всю эту дискуссию.
Первое. Автор поста прав в утверждении, что множество не может содержать повторяющихся элементов. By defenition.
И запись {1,1,1} — действительно некорректна, если {} — обозначает множество, то это множество может быть ТОЛЬКО {1}
Второе, из того, что автор прав в предыдущем пункте не следует, что он сделал правильный вывод. Таблица — это множество. Но не совсем обычное.
На основе понятия «множество», можно построить другие объекты, которые так же будут являться множествами, но при этом иметь другие свойства. С их помощью и можно описать таблицу.
Например, уже упомянутое мультимножество, в котором элементы имеют кратность. Для нашей задачи оно не подойдет, в таблице важен порядок.
Однако, еще немного математических преобразований позволяют получить такой объект как "кортеж". Кортеж — это упорядоченная последовательность элементов. И да, он может быть выражен используя только определение множества, и сам является множеством. Обозначение: "()", и судя по всему это именно то, что вы пытались выразить своим примером. Правильная запись «различных единиц» будет выглядеть как: (1,1,1,1)
Частным случаем кортежа является такой объект как "пара" — это просто кортеж из двух элементов.
На примере пары можно показать как получается упорядоченность. Пара (a,b) выражается через множество как { {(a)}, {(a), b} }, где (x) = {{/}, {/, x}}, {/} — пустое множество. Соответственно пара (b, b) -> { {(b)}, {(b), b} }. В русской википедии на этом месте ошибка, но можно глянуть в английскую.
А теперь давайте выразим таблицу, с помощью элементов выше.
В таблице есть строки и столбцы.
У каждого столбца есть имя, например «id», «name». Если вы хотите взять значения столбцов по определенной строке то вы получите набор пар:
((id: 1), (name: «Vasya Pupkin»)) — строка таблицы.
Но разумеется, у нас много строк, и их порядок важен. Поэтому в целом таблицу можно выразить как кортеж кортежей пар (название столбца, значение):
(
((id: 1), (name: «Vasya Pupkin»)),
((id: 2), (name: «Nikita Twink»)),
((id: 10), (name: «Petya Petechkin»))
)
И да, этот кортеж все еще можно выразить с помощью одного только понятия «множество». Но правильная запись займет весьма значительный объем (почему — можно узнать в уже упомянутой статье Tuples, английской википедии).
Разумеется, это всего один из способов описать таблицу математически через теорию множеств, но он самый интуитивно понятный, на мой вкус.
Но разумеется, у нас много строк, и их порядок важен.На момент выполнения запроса порядок строк неважен. Да и вообще, сам по себе SELECT без ORDER BY никакого определённого порядка не гарантирует.
Я просто очень давно не работал с таблицами.
Тогда вы правы и у них нет «порядка», но из этого будет следовать неразличимость двух строк с одинаковыми значениями. Если это так — описывать их кортежем избыточно, можно использовать мультимножество.
Если и для столбцов порядок избыточен, то и там не нужен кортеж. Можно описывать как множество пар, если названия столбцов уникальны — мы гарантируем уникальность каждой пары из набора.
Таким образом в случае когда порядок не важен (т.е. мы не можем сказать «столбец номер такой-то» и «строка номер такая-то») получим мультимножество множеств пар.
Т.Е. у строк нет какого-нибудь rowNumber, по которому ее можно выбрать не зная о ее содержании?Нету. Также, как нету отношений «следующая» или «предыдущая» строка и понятий «первая» и «последняя» строки. Это первая нормальная форма.
1. Нет упорядочивания строк сверху вниз (другими словами, порядок строк не несет в себе никакой информации).
2. Нет упорядочивания столбцов слева направо (другими словами, порядок столбцов не несет в себе никакой информации).
3. Нет повторяющихся строк.
4. Каждое пересечение строки и столбца содержит ровно одно значение из соответствующего домена (и больше ничего).
5. Все столбцы являются обычными (не скрыты от пользователя и не содержат каких-либо данных, доступных только по специальным функциям).
По п.1 всё зависит от реализации, но у строки всегда есть адрес, явный или неявный — вопрос реализации, для oracle это будет rowid, и его можно получить и даже использовать (но не всегда)
Usually, a rowid value uniquely identifies a row in the database. However, rows in different tables that are stored together in the same cluster can have the same rowid.
You should not use ROWID as the primary key of a table. If you delete and reinsert a row with the Import and Export utilities, for example, then its rowid may change. If you delete a row, then Oracle may reassign its rowid to a new row inserted later.
Русскую википедию (как и любую другую) очень легко исправитьНет. Попытки что-то править в русской википедии немедленно приводят к тому, что все изменения откатывают и проводят весь текст обратно к исходному ужасу.
Такое ощещение, что у них задача — привести всё к такому виду, чтобы неспециалист не мог понять ни-че-го. Текст, написанный на человеческом, понятном, языке — объявляется «неакадемичным» и нещадно вымарывается.
Потому Википедию я использую только английскую, в русскую поглядываю тогда, когда нужно давать ссылку… а править ошибки в продукте, которым не пользуешься — это перебор, как по мне…
Либо наоборот, точные научные определения заменяются на бытовые.Пример можете привести? Я такого не видел. В русской версии, по крайней мере.
В английской — да, там стараются вначале рассказать в «бытовых» терминах, понятных читателю, а длинное и точное определение для зануд — где-то внизу, отдельным пунктом. В русской же… оставь надежду, всяк сюда входящий…
В статье «Мясо» была (помимо прочих) война правок за определение.Тем не менее то, что там написано сейчас — это всё равно «очень академичное» определение, через которое нужно «прорываться с боем»: Мя́со — скелетная поперечно-полосатая мускулатура животного с прилегающими к ней жировой и соединительной тканями, а также прилегающей костной тканью (мясо на костях) или без неё (бескостное мясо).
Сравните с английской википедией: Meat is animal flesh that is eaten as food. Всё. Дальше — там об охотниках, о том, что мясо состоит, в основном, из воды, белков и жира. Много чего есть — но нет отправляющей в объятия морфея «академичности».
Само собой под мясом многие понимают исключительно мышцы и стремились протолкнуть именно такое бытовое понимание.Тем не менее редакторы успешно с этими поползновениями боролись и отстояли своё право превратить статью в ужас, от которого нормальный человек просто отвернётся.
Только не надо про то, что понятие «мясо» отличается в разных языках. Вот «академичная» (и почти уже забытая) Британника: Meat, the flesh or other edible parts of animals (usually domesticated cattle, swine, and sheep) used for food, including not only the muscles and fat but also the tendons and ligaments.
Тот вопрос, о котором долго думали и авторы Британники и русской Википедии — в английской Википедии просто исключён. Он даже не упоминается. Потому что Википедия — она не для специалистов. У товароведов может быть одно определение мяса, у юристов — другое… но обычные люди вообще не задумываются — включает в себя понятие «обычное мясо» сухожилья или нет. Мясо — оно мясо и есть, если хотите точно — наверное можете уточнить «бескостное мясо» или «мясо на косточке».
Так что извините, но… нет. Ваш пример только подтвердил очевидное: горбатого — могила исправит. Русская Википедия — это, увы, что-то, чем я пользоваться не хочу и не буду. И всем, что умеет читать по английски не рекомендую.
Да, в английской тоже есть перегибы (особенно если речь заходит о политических темах), но её, по крайней мере, интересно читать! Это не бесконечная «война с неакадемичностью», откуда ты пытаешься, с боями, выцепить что-то полезное, а живое и легко читаемое повествование. А для «академичности» — там есть ссылки на первоисточники.
Насколько я понимаю, энциклопедия это литература для широкого круга читателей, обозревающая все отрасли человеческого знания. Для отдельных заинтересованных читателей про мясо наверняка есть свой специализированный ресурс.
Предлагаете сделать википедию энциклопедией про все, кроме мяса? Вас там только мясо беспокоит?
Ну какую область человеческого знания обозревает статья про мясо?!))))
Ну какую область человеческого знания обозревает статья про мясо?!))))Посмотрите на статью в Wikipedia. Кулинария, диетология, история, религия и много чего ещё. Собственно всё это есть в обоих версиях — и в английской и в русской. Вот только английская — написана явно для человека, которого может заинтересовать как это чёртово мясо готовить (ну предположим индиец решил начать употреблять его в пищу и полез в Википедию...) а вот для кого написана русская статья — я вообще не понимаю.
Представить себе индийца, который не знает как готовить мясо — я могу. Русскоязычного… сложнее, но тоже могу. Представить себе человека знающего о том, что такое «поперечно-полосатая мускулатура животного» и «соединительная ткань», но не представляющего себе что такое мясо… ну не могу хоть убей.
Может быть это связано с культурными различиями в применении Википедии у нас и за рубежом?
Не знаю, как именно используется английская википедия за рубежом, но у нас ее на полном серьезе цитируют студенты в своих "научных" работах: курсовых, исследовательских, дипломных и т.п. Если на русской википедии будут неакадемичные термины, то они начнут просачиваться во все продукты жизнедеятельности творчества студентов и будут там неуместны.
Может быть это связано с культурными различиями в применении Википедии у нас и за рубежом?Вряд ли. Как раз более-менее специализированные статьи, которые описывают действительно сложные веди — это обычно достаточно добротный перевод с англоязычной Википедии (с иногда посаженными мелкими ошибками там где переводчик напутал), но чем проще предмет о котором статья — тем более «академичным» (и менее читабельным) становится текст.
Цитировать статью из Википедии в научной работе — это просто ужас же. Как можно цитировать то, что любой человек может исправить?
Википения содержит, слава богу, ссылки на первоисточники — вот их и цитируйте, если нужно.
Больше бесит пересечение, особенно с кругами Венна
Вот и стоит уточнить, слышал ли испытуемый про реляционную алгебру, и в каком смысле — пересечение.
ИМХО, круги Венна можно оставить, но внутри них допустимы только названия таблиц, а не элементы-цифирьки. Но только для inner join'а. Как наглядно и просто нарисовать в виде картинки, тот же left join — я не знаю.
По аналогии с вашим постом можно удивляться, что люди на вопрос «сколько будет 2х2?» отвечают «4» (в общем случае это, конечно же, не так), и говорить что «понимание умножения сломано»
Кто вам сказал такую глупость? Множество — это просто совокупность элементов. КАКИХ — зависит от того, что вам надо. В первом приближении всё можно считать множествами.
Тогда что получается: даны множества A={a, a, b} и B={a, b}. Думаю не будете спорить что a принадлежит A. Также А принадлежит B, а B принадлежит A (потому что каждый елемент левого множества принадлежит правому). Отсюда A=B. Имхо бессмысленная возможность иметь множества с не уникальными элементами.
Отсюда A=B. Имхо бессмысленная возможность иметь множества с не уникальными элементами.
вопрос в том, можете ли вы в множестве A различить первую a и вторую. Если можете, то никаких парадоксов нет: A не является подмножеством B. И множества не равны.
Если не можете, то у вас, по факту, множество A={a, b}
Как только я начинаю «различать» элементы, то они перестают быть уникальными.
Бинго! :) В точку! И это сразу решает все проблемы.
а не о своем понимании что такое уникальные элементы?
А что такое «уникальные элементы» в математическом смысле?
Множество — это просто совокупность элементов. КАКИХ — зависит от того, что вам надо. В первом приближении всё можно считать множествами.
И каким же образом в произвольном множестве вы будете отличать один элемент множества от другого, если они, буквально, одинаковые?
Во первых, множество.
Да, вот только таблица не простое множество, а упорядоченное, то есть, например, вот таблица {1,1,1} это не множество цифр, а множество двоек {[1,1],[2,1],[3,1]}.
Если уж докапываться до терминологии, то следует уточнять, что речь не про множества, а про отношения и реляционную алгебру.
А в отношении одинаковых кортежей все равно не бывает.
пересечение двух отношений в терминах реляционной алгебры, это и есть inner join
Дед, ты в маразме. Для join в реляционной алгебре есть операция соединения (сюрприз-сюрприз!), которая эквивалентна операции выборки из декартова произведения двух отношений (то есть множеств кортежей).
Если джойнов немного, и правильно сделаны индексы, то всё будет работать быстро. Проблемы будут возникать скорее всего лишь тогда, когда у вас таблиц будет с десяток в одном запросе. Дело в том, что планировщику нужно определить, в какой последовательности осуществлять джойны, как выгоднее это сделать.
Если чел — слабо разбирается в SQL и плохо представляет себе, что будет делать СУБД, а что такое план запроса — вообще не слышал. То в такой ситуации, как мне кажется, правильнее будет пихать все в джойны и считать, что СУБД умнее программера. Правило — эвристическое, но для новичков — работает :)
Это явно будет лучше, чем тысячи мелких запросов внутри цикла, или ручное склеивание таблиц средствами языка.
Ну а если чел знает что делать, то он разберется, как переписать запрос, чтобы ускорить его.
```
SELECT s.id, c.city
FROM users_stats AS s
JOIN cities_ip_ranges AS c
ON c.ip_range && s.ip AND s.ip > 2
```
но вроде и для ms sql на которой в основном 1с запускают тоже советуют.
А зря. Там и MAXDOP=1 советуют, не вникая в суть. Что тоже зря (это вырожденный случай, годный для определённого количества ядер процессора).
Это не так. Например, условие в join не считает поля отсутствующей записи правой таблицы равными null, потому что join на момент его работы ещё не выполнен, и условие примеряется к имеющимся строкам объединяемых джойном таблиц. А условие в where примененяется к сделанной выборке, после отработки всех join, то есть поля, выбранные из второй таблицы в тех строках, где подходящая строка во второй таблице не нашлась, заполнены значением null.
Это логика SQL, и любой оптимизатор, даже если он выполняет условия в другие моменты времени и в другом контексте, должен эту логику сохранять.
Для Oracle не работает, как пример распостранённая проблема, когда вы полагаетесь на то что в join вы выбрали только строку определённого формата а потом в where её преобразтвали к дате, к примеру.
По математическому определению, во множестве все элементы уникальны, не повторяются, а в таблицах в общем случае это вообще-то не так.
То есть, множество эквивалентных элементов — это уже не множество?
К вашему сожалению, в понятии множества нет такой характеристики, как уникальность.
Формально определение равенства множеств (в теории ZFC и других) не различает множества, имеющие поповторяющиеся элементы, то есть:
{ x } = { x, x }
Поэтому, хотя теория множеств явно не требует уникальности элементов (она даже об этом не упоминает) но с точки зрения выводов теории это не имеет практического смысла
но с точки зрения выводов теории это не имеет практического смысла
Это имеет практический смысл с точки зрения построения других математических конструкций. Например, нуль-мерные пространства — тоже не имеют практического смысла, но тем не менее существуют. И что?
Другое дело, что разработчики БД знают что человек слаб, поэтому часто вводят неявные поля типа ROWID.
Первая нормальная форма реляционной БД. Одно из условий — нет повторяющихся строк. Так что да, теория запрещает совершенно одинаковые кортежи в таблице.
1NF не про дубликаты кортежей, а про то, что в атрибутах мы не храним массивы данных.
According to Date's definition, a table is in first normal form if and only if it is «isomorphic to some relation», which means, specifically, that it satisfies the following five conditions:[12]
There's no top-to-bottom ordering to the rows.
There's no left-to-right ordering to the columns.
There are no duplicate rows.
Every row-and-column intersection contains exactly one value from the applicable domain (and nothing else).
All columns are regular [i.e. rows have no hidden components such as row IDs, object IDs, or hidden timestamps].
Плюс, нужно отличать 1NF для отношения ( на самом деле отношение всегда в первой нормальной форме) и 1NF для таблицы, как способа записывать отношения.
Например, тот же IP-адрес — это на самом деле структура из 4 октетов. Должны ли мы хранить их в отдельных колонках?
Если для в нашем домене какая-то структура рассматривается как атомарный объект — то его теоретически можно хранить в одной колонке. Например — мы в таблице логируем ответы от сервера. Сервер отвечает каким-то json-нами, но нам совершенно не интересно что внутри этого json. Поэтому мы запихиваем его в колонку и не паримся. И это не нарушает 1NF. Ровно до тех пор, пока мы не захотим обращаться к элементам внутри этого json.
Например, тот же IP-адрес — это на самом деле структура из 4 октетов.
Это одно 32-битное поле. См. структуру заголовка пакета.
Отображение в виде 4 октетов в десятичной записи сделано исключительно для чтения человеком.
Тогда вот вам другой подход — до введения CIDR из IP-адреса можно было однозначно выделить адрес сети и адрес хоста. Т.е. внутри IP-адреса все-таки была структура.
Ну или в качестве примера можно взять Ethernet MAC-адрес. Или GUID. С одной стороны для большинства применений — это просто цепочка октетов и пофиг что там внутри. Но с другой стороны — они таки имеют внутреннюю структуру. Соответственно, если применять 1NF бездумно и настаивать на полной атомарности данных — то их всегда надо хранить в отдельных полях.
Уникальность это мутная штука когда значения не являются дискретными. Зато там есть аксиома выбора, которая обеспечивает подобное свойство.
Вы наверное про бесконечнозначное представление
f3.1415926…
или r если рациональное (далее идут a/b)
r100/777
Очевидно рациональные числа сравниваются за конечное время хотя в общем виде конечно это не так
Вот поэтому вместо равенства используется аксиома выбора. Возможность отличать один элемент от другого и вытаскивать по одному просто постулируется. Как это будет реализовано для конкретных объектов уже ваша проблема.
Влияет. Иначе нельзя было бы рассуждать о множествах вещественных и рациональных чисел, множествах бесконечных величин и т.п. не уперевшись на старте в то, о чем вы пишете. Аксиома абстрагирует множества от этих вот деталей.
Постулировать можно только само равенство, но не разрешимость проверки равенства.
Я тут писал habr.com/ru/post/445904
(раздел «Малоизвестные факты»)
Сорри за занудство про теорию множеств, но сами понимаете, в интернете ктото неправ, я вынужден действовать)
Во-первых, таблица — это вообще не множество. По математическому определению, во множестве все элементы уникальны, не повторяются, а в таблицах в общем случае это вообще-то не так. Вторая беда, что термин «пересечение» только путает.
На сколько я помню, то теория рел. БД говорить что таблица — это множество кортежей. Разные кортежи могут хранить одинаковые значения и тогда это эквивалентные кортежи, но все же разные. Поэтому нет никакого противоречия, так как все элементы таблицы уникальны по определению.
Что вас заставило сомневаться в том, что люди, приходящие на собеседования, могут быть образованнее вас?
Декартово произведение (Cartesian product, cross join) в реляционной алгебре и в теории множеств работают немного по-разному. Но на уровне логики (формальной) смысл операций один и тот же. Поэтому круги Венна читаются однозначно, даже на уровне деталей, если есть понимание в рамках какой модели строятся рассуждения.
Что вас заставило сомневаться в том, что люди, приходящие на собеседования, могут быть образованнее вас?
Интересно, где вы это в статье увидели? Между строк?
Надо вдумываться в то, что говоришь на собеседовании, а не повторять бездумно заученные фразы. Inner Join явно не «пересечение 2-х множеств». Пример в статье это показывает.
Вот честно, не представляю, как кругами можно кому-то объяснить декартово произведение. Об этом и статья.
Кругами хорошо показывать пересечение отношений (intersect в sql), а не декартово произведение (join в sql)
По моему опыту:
INNER и LEFT джойны нужны почти всегда.
RIGHT JOIN нужен редко.
FULL OUTER нужен редко.
CROSS не нужен почти никогда, даже NATURAL JOIN нужен чаще чем CROSS.
Декартово произведение нужно, например, чтобы в HIVE джойнить по битовой маске или по попаданию значения из одной таблицы в интервал, задаваемый колонками из другой таблицы. Из коробки не получается.
right join используется, когда раньше был inner, но ситуация изменилась
full join — реальная ситуация:
1. например, нужно для одного клиента с разных счетов суммы с баланса вывести
2. или взять остатки товара с розницы и со склада
cross join — есть банда кустомеров, для них есть 1 тариф и всё такое
Да полностью согласен, что нужно СУБД довести до состояния строго учителя математики, который лупит по рукам железной линейкой за каждый шаг в неверном направлении, но люд нынче пошёл нежный, и он сразу взвопит, что его унижают, лишают свободы, а после этого развернёт знамёна и уйдёт на монгу… Нет ну правда, СУБД имеют дело именно с множествами, просто в случае плохо организованной базы, СУБД не может различить одну единицу от другой, поскольку она не в курсе, что делают одинаковые данные в разных записях одной таблицы. Она милостиво делает по этому безобразию декартово произведение и выдаёт это пользователю, в надежде, что тот сможет достучаться до печени DBA, с целью приведение схемы в божеский вид. Уважаемого автора устроило бы падение базы с дампом памяти по типу деления на ноль?
JOIN идет далеко не всегда по первичному ключу,
Я более того скажу — не всегда это нужно. Например, иногда я хочу, чтобы в результате джойна записи «размножились». Например, у меня есть таблица номенклатуры и характеристик. И я хочу по какому-нибудь правилу получить все допустимые пары номенклатура-характеристика.
Дальше чаще всего оптимизатор сам разберется, разве что с покрывающими индексами по крайней мере SqlServer любит перебдеть сильно в своих хинтах о индексах.
Как мне кажется, не стоит использовать диаграммы Венна для объяснения джойнов. Также, похоже, нужно избегать термина «пересечение».
Круги Венна прекрасно объясняют суть, не надо от них отказываться. Но они про отношения в терминах реляционной алгебры, а не про некие абстрактные множества. Отношения конечно тоже множества, но с многими дополнительными свойствами. Если про это забыть то получается некий беспорядок про который вы пишете. Если же говорить про множества то Join это их умножение, а не пересечние. Остальное — inner, outer, on это, как вы правильно пишете, синтаксический сахар добавленный в язык SQL из практических соображений. Всетаки парсеры и оптимизаторы запросов не настолько умны чтобы эффективно превратить ветхозаветное но строго по Кодду
select t1.id,t2.id
from t1,t2
where t1.id=t2.id
union
select id, null
from t1 where id not in (select id from t2)
в красивое и которое еще и подскажет оптимизатору запросов чего программист на самом деле хочет
select t1.id,t2.id
from t1
left join t2 on t1.id=t2.id
но лет 20 назад приходилось писать по первому варианту или использовать специфический синтаксис конкретной СУБД. Вот для Oracle например
select t1.id,t2.id
from t1,t2
where t1.id=t2.id(+)
Во-первых, таблица — это вообще не множество
А что же это? C математической точки зрения?
По математическому определению, во множестве все элементы уникальны, не повторяются, а в таблицах в общем случае это вообще-то не так
Интересен источник данного определения и был бы благодарен, если бы вам удалось то, что не удалось моему преподавателю математического анализа — дать строгое математическое определения понятия «множество».
Должно быть так

дело в том, что если единичек будет по 3 штуки, то в пересечении должно быть 9 штук
а если по одной, то только одна
У вас просто начальная посылка неверная, а из ложной просылки любой вывод ложен.
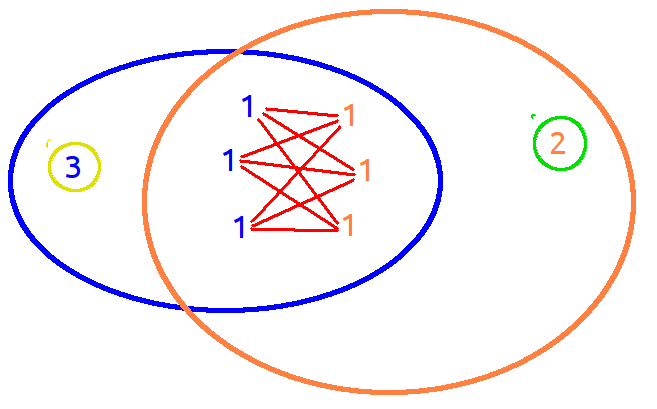
Красные линии – строки, которые будут результатом inner join; они будут так же и в left join, и в right join.
Золотой круг – строка, которая будет дополнительно в left join.
Зелёный круг – строка, которая будет дополнительно в right join.
Но всё же при join нескольких таблиц правильнее было бы рассматривать N-мерную таблицу (по количеству таблиц, участвующих в join).
С трёхмерными и более всё чуть более сложно, но простой двухмерный вариант вполне можно изобразить:
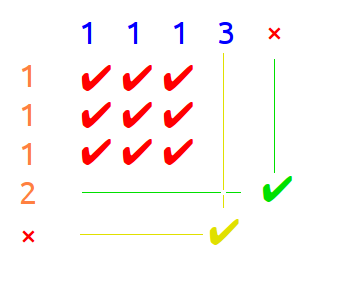
Думал, это перевод старой статьи Лукаса. Оказалось, что нет.
Но как??
Специально сейчас заморочился, поспрашивал. Я не знаю, кого вы там собеседуете, но ни у одного из опрошенным мной моих знакомых (кто хоть сколько-то имел практики в sql) не возникло сомнений, что записей будет четыре. И ни один из них даже не слышал про какие-то там "пересечения множеств".
Если использовать для объяснения, то мне кажется объяснить один термин «декартово произведение» на порядок проще чем объяснять отдельные типы join'ов
Ответ про множества действительно неверный, потому что джоины не удаляют дубликаты. Ну и странно, что кандидаты считаю возможным джион только по айдишкам.
Запрет на джоины бывает не от того, что они тормозят, а из-за шардинга базы. Часть таблицы на этой ноде, часть на другой.
Ну и добавлю, что у кандидатов действительно проблемы с сырым sql после всяких Джанго-ОРМ.
Но зачем разработчикам знать нюансы терминологии теории множеств на собеседовании по SQL на стандартном базовом вопросе про SQL?!
Не знает отличий между INNER и LEFT — не писал в SQL запросы сложнее «дай список по таблице с фильтром» — надо учить или прощаться.
Знает разницу между INNER и LEFT — ок, даже кружочками (привет универ, или гугл, или 100500 других источников знаний по SQL). Хотите уточнить пределы знаний — задаете дальнейшие вопросы. Про не уникальность, про сравнение NULL, да про что угодно вплоть до оконных функций, и вставки в несколько таблиц одним INSERT запросом
задаете advanced вопросы? это точно из
Есть подозрения, что причина в том, что в большинстве учебных заведений теорию БД преподают с точки зрения реляционной модели и недостаточно хорошо проговаривают ее отличие от модели, принятой в SQL. В классической реляционной модели, как она была описана Коддом, отношения содержат только уникальные кортежи, поэтому описанная проблема в принципе не существует.
Поэтому (это уже автору) корректно не задавать вопрос «чем отличаются», так как отличаются — синтаксисом (LEFT=/=INNER) и формально этот ответ верен, а чем будет отличаться результат выполнения запроса или каким он будет на конкретной схеме/данных. Ну или спрашивать еще, как много сказали выше :).

На этой картинке никто не подписывал какой-то конкретный набор строк как таблицу, все раскрашенные области явно относятся только к их соединениям.
Отличия от кругов скорее косметические.
Отсылка к диаграмме Венна имеет смыл только для тех кто помнит диаграммы Венна. Помнящих не так много как может показаться :D
Ни круги, ни прямоугольники не показывают наглядно почему будет 4 записи при наличии 2х единичек с каждой стороны и 6 записей при 2 к 3. Впрочем никакие картинки это нормально не показывают. При не уникальных записях мы получаем мультипликативный эффект. Чтобы его понять надо с другой стороны подходить к JOIN и построению запросов. Уж точно не пытаться это объяснять через cross join, использующийся примерно в 1 запросе из 10000.
По моему опыту проще заходит объяснение через вложенные циклы.
Но повторюсь, это уже гораздо дальше простого понимания когда надо ставить INNER, когда LEFT OUTER, а когда FULL OUTER, а именно на это нацелены картинки.
вы получите больше строк ответа, чем ожидается на основании этой картинки.
На этой картинке есть эти дубликаты, они будут в full outer join.
Кривая статья.
Таблица 1
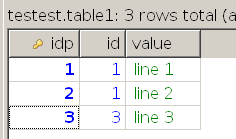
Таблица 2
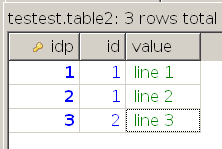
Вывод по inner join:
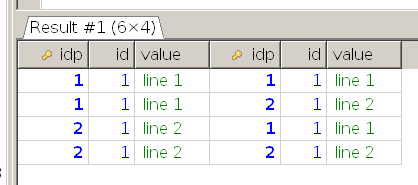
Что собсна криво? 1 встречается в таблице 1 два раза, как и в таблице 2 два раза.
Далее 2х2 дает 4 результата.
Если я поменяю вот так вот данные в таблице 2:
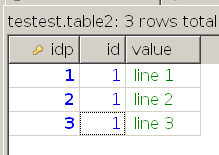
То получу:
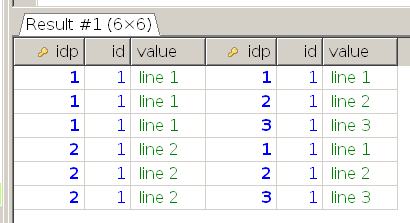
Где ON table1.id = table2.id
Вот с табличками:
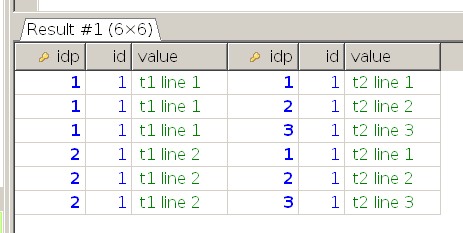
в этой статье вы узнаете правду, которая сломает ваш мозг и вам дальше с этим жить.
Это только в евклидовом пространстве 2*2=4, а в неевклидовом может быть и больше!
да, я знаю, что 99% не оперируют в неевклидовом пространстве ни в быту, ни на работе,
но у меня вот проектик — и там как раз оно — неевклидово.
Проблема в том, что любой join — это декартово произведение (возможно с добавлением null, если это не inner join). Потом этот уже join фильтруется по условию. Если этого не понимать, то реальность может укусить за задницу в самый неожиданный момент.
Кстати, Еще маленький совет по производительности. Если нужно просто найти элементы в таблице, которых нет в другой таблице, то лучше использовать не 'LEFT JOIN… WHERE… IS NULL', а конструкцию EXISTS. Это и читабельнее, и быстрее.
Читабельность — ок. Но чем быстрее — можно подробнее? Во всех ли случаях одно будет быстрее другого и есть ли вообще разница? Если да, то в каких СУБД?
Но если оптимизатор не в курсе что равенство Not Nullable-поля NULL равносильно отсутствию записи — то вариант с EXISTS и правда будет быстрее.
А если оптимизатор не умеет нормально работать с подзапросами — то быстрее может оказаться уже LEFT JOIN.



-Неделайте так"
Не надо писать код, который не очевиден для 99% программистов. Это с высокой вероятностью приведет к тому, что в код будет внесен баг рано или поздно. Код, простите за баян, надо писать так, будто поддерживать его будет склонный к насилию маньяк.
Понимание джойнов сломано. Это точно не пересечение кругов, честно«пересечение кругов» — это не сам джойн, а только его условие.
Из всех вариантов «корректного объяснения джоинов на картинке» мне понравился вариант Evir:
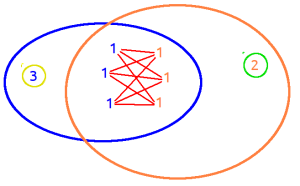
Но на нём слишком много элементов, можно упростить просто взяв любую картинку с «пересечением» и добавить на неё знак умножения:

Тогда если у человека, проводящего собеседование, останутся вопросы, то можно легко объяснить, что «пересечение» таблиц будет происходить на основе «условия джойна», а дальше будет «декартово произведение» всех попавших под условие элементов.
Т.е. для примеров из статьи:
JOIN {1,1,2} и {1,1,3} = {1,1}x{1,1} = {(1,1), (1,1), (1,1), (1,1)}
LEFT JOIN {1,1,2} и {1,1,3} = {1,1}x{1,1} + {2}
RIGHT JOIN {1,1,2} и {1,1,3} = {1,1}x{1,1} + {3}

В этом случае иногда бывает выгодно вынести часть запроса в подзапрос CTE; например, если вы точно знаете, что, поджойнив две таблицы, мы получим очень мало записей, и остальные джойны будут стоить копейки.
В общем случае это неверно. Не знаю, как там в Постгре, а вот в MS SQL, например, CTE (если не рекурсивный) — это просто синтаксический сахар для удобства написания, и при выполнении будет развернут в подзапросы, соответственно оптимизатор соединит их, как посчитает нужным, и вы сохраните все те же проблемы с множеством соединяемых таблиц.
Не раз и не два уже оптимизировал запросы именно за счет избавления от CTE и перевода их в лоб на временные таблицы, которые, действительно, будут выполняться последовательно, и для заполнения каждой временной таблицы будет свой отдельный план выполнения.
Во-вторых, самое близкое к джойнам (в случае внутренних — так вообще точное определение) теоретико-множественное понятие — это отношения: ru.wikipedia.org/wiki/%D0%9E%D1%82%D0%BD%D0%BE%D1%88%D0%B5%D0%BD%D0%B8%D0%B5_(%D1%82%D0%B5%D0%BE%D1%80%D0%B8%D1%8F_%D0%BC%D0%BD%D0%BE%D0%B6%D0%B5%D1%81%D1%82%D0%B2)
Множества, алгебра, картинки…
Я очень давно теорию изучал и нифига не помню определения, особенно теоретические. Но для себя оставил в голове практическое определение, через которое не мало раз объяснял селекты джунам…
Join объединяет записи из двух таблиц, при этом для каждой записи в одной таблице подбираются записи из другой. Вид джойна определяет способ отбора записей в объединённый результат. Left/Right Join — все записи из одной таблицы объединяются с найденными по условию из второй таблицы, а где не нашлось, подставляются пустые строки. Inner Join — то же самое, но без добавления пустых строк. Full — добавляются строки для обеих таблиц. Причём, если условие связи таблиц не определено — подходят все записи.
Ключевое тут — множественное число. Т.е. движок бд «постарается» вытащить всё, что сможет, ибо условия — это ограничения.
Представьте, что вы на свадьбе.
INNER JOIN — если со свадьбы выходят только семейные пары.
LEFT JOIN — если со свадьбы выходят семейные пары и ещё любовницы мужей.
RIGHT JOIN — если со свадьбы выходят семейные пары и ещё любовники жён.
FULL OUTER JOIN — если со свадьбы выходят семейные пары и все любовники и любовницы жён и мужей из семейных пар.
CROSS JOIN — ну это вот…
А каким должно быть соединение чтобы туда стали попадать любовники и любовницы — представить не могу.
Какой ответ ТС ожидает получить от собеседуемого об APPLY?
КАК это нужно показать на пальцах?
ЗЫ
Я, честно признаться, не очень понимаю валидность этих технических оффлайновых собеседований.
У меня на гитхабе выложен пет-проект по расчёту сальдооборотов для домашнего учёта.
Там всё ок.
Последние несколько лет работаю программистом БД, реально бизнес-логику пишу.
+ рефакторинг и оптимизация легаси.
НО.
Возможно, я интроверт. Или панические атаки случаются.
Последний раз на собеседовании я не смог на бумажке к схеме СКОТТ элементарный запрос написать.
Хотя на работе на доске я, бывает, примерно такие запросы пишу.
Кто-то видел???
Предполагаю, что операции пересечения множеств могут быть полезны для тестирования регрессии запросов.
Допустим есть некий запрос, который создает таблицу по сложным правилам.
Для тестирования готовятся эталонные данные и результат. Затем на эталонных данных прогоняют запрос и сравнивают фактический результат и эталонный.
При этом нужно будет понять, какие появились неожиданные записи и какие ожидаемые записи исчезли.
Таблица не множество
Уже неоднократно было замечено что множество. Хотя это дело подхода. Есть теоретико-множественный подход и там таблица это множество.
В этом смысле Ваши примеры некорректны т.к. в теории реляционных отношений нет таблиц
field
===
1
1
1
1
Хотя в реальной база данных такая таблица может существовать, но это ошибка проектирования таблицы т.к.потом приводит к неоднозначным результатам (например когда одну из единиц нужно удалить или поменять на 2)
По поводу join vs where то как утверждают в частности по postgresql нет разницы по скорости выборки. Речь идет о семантическом (не люблю козырять этим словом но в данном случае по-другому не скажешь) различие. where задает фильтр а join условие соединения. То есть если в join будут только первичные и внешние ключи а в where будут дополнительные условия фильтрации то запрос от этого будет более понятным.
Раз уже зашел разговор о скорости выборки и о postgresql то параллельно замечу что в отличие от других баз данных postgresql не создает индексов при создании свзи между таблицами (как это делает mysql) их нужно всегда дополнительно создавать вручную иначе будут тормоза.
По поводу диаграмм Венна нужно просто попытаться понять тех кто их рисует. Они относятся к ключам (без разницы внешним или внутренним) соединения:
таблица1 ключи {1,2,3,4}
таблица2 ключи {2,2,4,4,6,8}
inner join это пересечение то есть {2, 4}
left join это объединение левой таблицы с пересечением {1,2,3,4}
full join пересечение двух множеств ключей {1,2,3,4,6,8}
Спасибо.
Я сталкивалась на собеседованиях с вопросами вроде, «если все так, как вы объяснили про Left join (с помощью кружочков), то почему строк в итоговой выборке не столько, сколько в левой таблице»? Начинаешь там рассказывать про строки с Null и все такое… но тогда с описанием-кружочками не бьется.
А какие под капотом алгоритмы для INNER JOIN используются и каким образом достигается более высокая производительность в отличии от CROSS JOIN?
Очевидно, автор математически безграмотен, иначе бы он знал, что реляционные БД прекрасно описываются алгеброй отношений, которые работают на множествах. В частности, join - это есть декартово произведение двух множеств, и результатом этой операции является множество пар значений из этих множеств, а отличия различных join-ов прекрасно описываются множественными операциями (пересечение, объединение, разность) и диаграммами Вена (которые общепризнано применимы ко множествам). Поднимать холивар на эту избитую тему, и мучить своих коллег "каверзными" вопросами, который уже давно решены более умными и грамотными людьми, это есть продукт невежества и высокомерия автора. К сожалению, среди программистов такие уникумы встречаются слишком часто. Ребята программисты, сначала кончайте мех-мат, потом ит, будете грамотными специалистами без провалов в образовании, либо кончайте ит и не лезьте в теоретическую часть, вы можете, конечно, потихоньку её грызть, но не вываливайте наружу своё недопонимание каких-то моментов, ну, или будьте в этом вопросе деликатны.
Понимание джойнов сломано. Это точно не пересечение кругов, честно