I thought my previous post rather funny, and was surprised seeing it initially receive so few views. I thought the entertainment flopped, but fortunately I was wrong. I therefore feel it my duty before my readers to address the subject of the Landau & Lifschitz proof of the invariance of the interval.
You can find the summary of it in Wikipedia. Making their starting point the light-like interval always being equal to zero, Landau & Lifschitz seem to make a great fuss about it. The Wikipedia article even says: ‘This is the immediate mathematical consequence of the invariance of the speed of light.’ No, it is not.
I beg everyone’s pardon, but the light-like interval always being equal to zero is nothing else but the following statement: ‘The length of a ray of light will always be equal to the length of this ray of light’. Sounds like a cool story, bros and sis, but I cannot see what further inferences can be drawn from it. The ‘proof’ of this truism cannot fail under any circumstances whatever – whether you keep the speed of light invariant, or keep or change the metric of space or time or both – or make both metric and speed of light change – the light-like interval will remain equal to zero. I am okay with anyone wanting to prove it if they feel like it, but you cannot make it an ‘immediate mathematical consequence of the invariance of the speed of light’. Neither is it possible to make the constancy of the speed of light a consequence of the invariance of the light-like interval for the reason already mentioned: this is a truism. It does not prove anything, nor can it be a consequence of anything. When Landau & Lifschitz insist that this is a consequence of the constancy of the speed of light, that is either an error or a downright subterfuge, a means employed to create a spectre of logical connection between two unconnected notions, and charge this ghostly connection with pretended significance. And, since the following proof of invariance of an arbitrary interval hangs on the invariance of the light-like interval, we can altogether dismiss it: the necessity of introduction of such a measure as interval cannot be derived from the statement that a length of something will be equal to itself in whatever frame of reference it is measured.
For today’s topic now. We need this preliminary discussion to get prepared for the final of this longish saga.
In 1910, Varićak discovered that one can introduce an additive measure directly corresponding to the velocity in the place of the Einstein non-additive velocities – later, this measure c artanh(v/c) came to be known as ‘rapidity’.
What can this additivity of rapidity mean?
For the simple case of the parallel motion, Einstein (Einstein, p. 11) is very straightforward when deducing the formula of the velocity addition. His derivation is done for a more general case of coplanar velocities – we do not need this, and will be discussing an even simpler case of parallel velocities, but reproducing Einstein’s logic. He is considering a point moving relatively to the moving frame of reference at a speed w, and its coordinate x' is changing as x' = wt', whence, if x' = γ(x – vt) and

we get

or

the right-hand part of (1) being the formula for the resulting speed of the point in the unprimed frame of reference k (velocity addition) in the Einstein mathematics.
This straightforwardness, however, is a little puzzling. It looks okay to consider motion of a point, but add a second point located at the infinitesimal distance dx' to the first one, and you will get that your parallel translation does not preserve distances (and therefore stops being a parallel translation). But it is not what we are after today.
To get to the bottom of this velocity composition, let us suppose that what Einstein means by x' = wt' is nothing else but the function x' = (w/c)ct' in the (ct', x', y', z') coordinate system in a 4-space of hyperbolic curvature, or to be even more exact, the graph of this function drawn in this coordinate system. In that case, w/c should be the hyperbolic tangent of the angle between the graph line and the ct' axis, and that in its turn would mean that the ‘velocity addition’ problem is about finding the hyperbolic angle between the graph line and the ct axis, or the tangent of that angle.
Indeed, in the Einstein velocity addition formula one can easily recognize the sum of two area hyperbolic tangents:
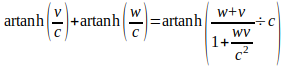
whence the new tangent u/c resulting from the ‘added velocity’ w will be

We can go further and see that the form of (2) suggests that the motion of k' is also being considered as a graph of the function x = (v/c)ct in the (ct, x) plane. Velocities being non-additive become clear in this perspective: if we need to find a sum of two angles, it will be useless to add up their tangents. Velocities are non-additive because they are tangents, and the rapidity c artanh(v/c) is additive since it is the angle.
This passing remark, though rather elementary, will be helpful for the discussion to come.
To be continued
Literature
[1] Einstein, A. On the Electrodynamics of Moving Bodies; available here
[2] Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields. Course of Theoretical Physics. Vol. 2
[3] Varićak, V. Anwendung der Lobatschefskijschen Geometrie in der Relativtheorie, found here
Previous parts
Following part
Let’s Discuss the Lorentz Transforms – Part the Last: The Real Derivation, or The Nail in the Casket