Лог-линейные модели и их представления в виде марковских сетей позволяют показать структуру взаимосвязей между случайными величинами. Однако полученная визуализация может оказаться трудна для восприятия из-за большого числа равнозначных ребер в графе такой модели. При работе с порядковыми и бинарными переменными гауссовы копулы (Gaussian copula graphical models, сокр. GCGM) дают возможность повысить наглядность и упростить интерпретацию модели. В статье приведен краткий обзор теории и построен пример GCGM для European Social Survey данных.

Всем доброго времени суток. Недавно прочитал статью про имитационный отжиг на примере задачи коммивояжера. Картинка до и после оптимизации вызвала интерес. Чем-то подобные вещи заманивают.Также в комментариях заметил, что людям было бы интересно посмотреть на сравнение с другими видами оптимизации.

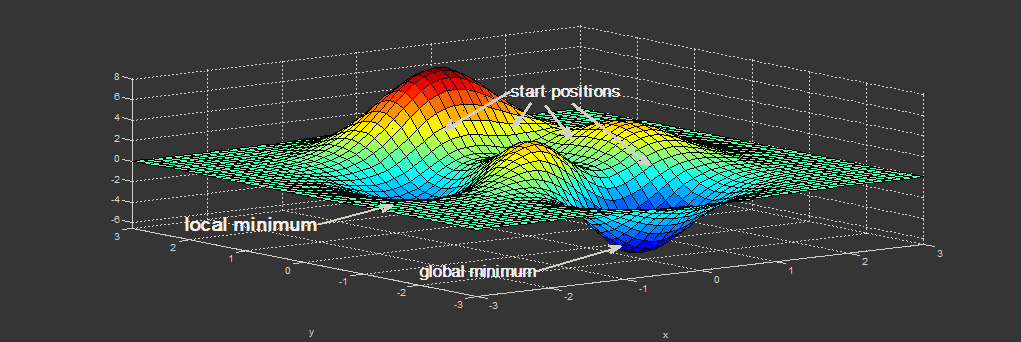
Нахождение экстремума(минимума или максимума) целевой функции является важной задачей в математике и её приложениях(в частности, в машинном обучении есть задача curve-fitting). Наверняка каждый слышал о методе наискорейшего спуска (МНС) и методе Ньютона (МН). К сожалению, эти методы имеют ряд существенных недостатков, в частности — метод наискорейшего спуска может очень долго сходиться в конце оптимизации, а метод Ньютона требует вычисления вторых производных, для чего требуется очень много вычислений.

Для устранения недостатков, как это часто бывает, нужно глубже погрузиться в предметную область и добавить ограничения на входные данные. В частности: МНС и МН имеют дело с произвольными функциями. В статистике и машинном обучении часто приходится иметь дело с методом наименьших квадратов (МНК). Этот метод минимизирует сумму квадрата ошибок, т.е. целевая функция представляется в виде

Алгоритм Левенберга — Марквардта является нелинейным методом наименьших квадратов. Статья содержит:

• объяснение алгоритма
• объяснение методов: наискорейшего спуска, Ньтона, Гаусса-Ньютона
• приведена реализация на Python с исходниками на github
• сравнение методов

Иногда при разработке программного обеспечения требуется встроить дополнительную функциональность в уже существующие приложения без модификации исходного текста приложений. Более того, зачастую сами приложения существуют только в скомпилированном бинарном виде без наличия исходного текста. Широко известным способом решения указанной задачи является т.н. “сплайсинг” – метод перехвата функций путем изменения кода целевой функции. Обычно при сплайсинге первые байты целевой функции перемещаются по другим адресам, а на их исходное место записывается команда безусловного перехода (jmp) на замещающую функцию. Поскольку сплайсинг требует низкоуровневых операций с памятью, то он осуществляется с использованием языка ассемблера и С/C++, что также накладывает определенные ограничения на реализацию замещающих функций – они обычно также реализованы на С/C++ (реже на ассемблере).

Метод сплайсинга для перехвата API-функций в Windows широко описан в Интернете и в различных литературных источниках. Простота указанного перехвата определяется следующими факторами:

1. целевая функция является статической – она сразу присутствует в памяти загруженного модуля;
   
2. адрес целевой функции легко определить (через таблицу экспорта модуля или функцию GetProcAddress).
   

Реализация замещающих функций на C/C++ при перехвате API-функций является оптимальным вариантом, поскольку Windows API реализовано, как известно, на языке C, и замещающие функции могут оперировать теми же понятиями, что и заменяемые.

Как может показаться, анализ сигналов и данных — тема достаточно хорошо изученная и уже сотни раз проговоренная. Но есть в ней и некоторые провалы. В последние годы словом «энтропия» бросаются все кому не лень, толком и не понимая, о чем говорят. Хаос — да, беспорядок — да, в термодинамике используется — вроде тоже да, применительно к сигналам — и тут да. Хочется хотя бы немного прояснить этот момент и дать направление тем, кто захочет узнать чуть больше об энтропии. Поговорим об энтропийном анализе данных.

Всем привет!

Меня зовут Алексей Бурнаков. Я Data Scientist в компании Align Technology. В этом материале я расскажу вам о подходах к feature selection, которые мы практикуем в ходе экспериментов по анализу данных.

В нашей компании статистики и инженеры machine learning анализируют большие объемы клинической информации, связанные с лечением пациентов. В двух словах смысл этой статьи можно свести к извлечению ценных крупиц знания, содержащихся в небольшой доле доступных нам зашумленных и избыточных гигабайтов данных.

Данная статья предназначена для статистиков, инженеров машинного обучения и специалистов, которые интересуются вопросами обнаружения зависимостей в наборах данных. Также материал, изложенный в статье, может быть интересен широкому кругу читателей, неравнодушных к data mining. В материале не будут затронуты вопросы feature engineering и, в частности, применения таких методов как анализ главных компонент.

Источник.

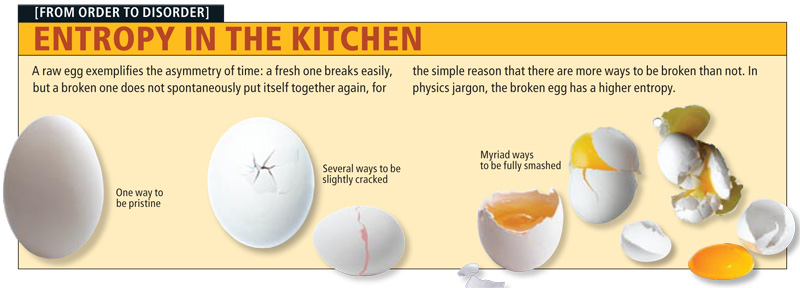
А не замахнуться ли нам на Эдсгера нашего Дейкстру?

В первой части мы описали способ ранжирования симметрично связанных объектов (узлов неориентированного графа) относительно заданного направления. Для каждого объекта (узла) вычисляется потенциал (лапласиана), который определяет его положение относительно заданных источника и цели. В данной статье мы покажем, как потенциалы упрощают задачу поиска кратчайших путей (оптимальных маршрутов). А также как меняются сами потенциалы при изменении внешних условий.

В общем случае минимизируемая величина — это необязательно расстояние, — весами ребер графа могут быть стоимости, штрафы, убытки, времена, — любые величины, которые можно складывать. Задача является классической, наиболее простой алгоритм поиска кратчайшего пути дал Э. Дейкстра в 1959 году.

… Молвит он: «Коль жив я буду, чудный остров навещу, у Гвидона погощу».

В царстве Салтана не без изьяна. Принят закон — не лезть за кордон, да тут князь Гвидон.
Опять прислал поклон, да приглашение на угощение,- надо принимать политическое решение.

Дворцовые интриганки, похожие на поганки, встали стеной — «мол, скажи, что больной». Но прослышал Салтан про Гвидонов кальян, про изумрудную белку, да богатырскую стрелку. А главная новинка — молодая жинка. В общем, ехать решено — «Я не был за морем давно».

Было однако одна проблема,- нужен был маршрут или схема. Поскольку никто (кроме Врангеля барона) не знал, как добраться до острова Гвидона. Корабельщики дали карту,- пришлось сесть за парту. Над картой склонился Салтан, — где тут остров Буян? Задача была как будто знакома — проложить путь к острову Гвидона. Но как найти дорогу, когда путей слишком много?

До ночи решал Салтан задачку, в итоге свалился в спячку. Снились ему матрицы и точки, да на болоте кочки. На кочку прыгнул Нео с острова Борнео.
— Если хочешь добраться ко сроку — плыви по максимальному потоку.
— Чего? — Салтан почти проснулся. Но Нео уже в зайца обернулся.

Статья рассчитана в первую очередь на новичков и тех кто только собирается опубликовать свой первый проект на GitHub. Те у кого уже есть опубликованные проекты также могут почерпнуть что-то полезное и написать свои лучшие практики в комментариях. В статье представлены пять простых советов как улучшить ваш GitHub проект.

На первый взгляд, dynamic в C# — просто object с поддержкой машинерии компилятора. Но не совсем.

Ядром времени выполнения является DLR (Dynamic Language Runtime) — подсистема/фреймворк для поддержки динамических языков программирования. Существует реализация под собственно C#, который идет в поставке с .NET, и отдельная для Iron-языков.

Когда мы работаем с обобщениями (generics), то CLR имеет свои оптимизации на предмет специализации оных. В тот момент, когда CLR+DLR должны работать с generics вместе, поведение написанного кода может стать непредсказуемым.

Как вы думаете, чего в апельсине больше — кожуры, или, хм, апельсина?



Предлагаю, если есть возможность, пойти на кухню, взять апельсин, очистить и проверить. Если лень или нет под рукой — воспользуемся скучной математикой: объем шара мы помним из школы. Пусть, скажем, толщина кожуры равна от радиуса, тогда , ; вычтем одно из другого, поделим объем кожуры на объем апельсина… получается, что кожуры что-то около 16%. Не так уж мало, кстати.

Как насчет апельсина в тысячемерном пространстве?

Пойти на кухню на этот раз не получится; подозреваю, что формулу наизусть тоже не все знают, но Википедия нам в помощь. Повторяем аналогичные вычисления, и с интересом обнаруживаем, что:

• во-первых, в тысячемерном гиперапельсине кожуры больше, чем мякоти
• а во-вторых, ее больше примерно в 246993291800602563115535632700000000000000 раз

То есть, каким бы странным и противоречивым это ни казалось, но почти весь объем гиперапельсина содержится в ничтожно тонком слое прямо под его поверхностью.

Начнем с этого, пожалуй.

«Три девицы под окном пряли поздно вечерком.»



Ну как пряли. Не пряли, конечно, а лайкали друг на друга. По условиям конкурса «мисс Салтан» девицы должны были выбрать меж собой лучшую.

«Какой-то странный конкурс», — беспокоились девицы. И это было правдой. По правилам конкурса вес лайка участника зависел от того, сколько лайков он получает от других. Что это значит, — никто из девиц до конца не понимал.
«Как все сложно», — тосковали девушки и подбадривали себя песней «Кабы я была царицей».

Вскоре «в светлицу вошел царь — стороны той государь» (показан на рисунке). «Во все время разговора...», — ну понятно в общем.
«Собираем лайки нежности — формируем матрицу смежности», — бодро срифмовал он.
Девицы-красавицы с именами Алена, Варвара и Софья засмущались, но лайки (из балалайки) передали.

Вот что там было:

• Алена получила 1 лайк от Софьи и 2 лайка от Варвары.
• Варвара получила по лайку от Алены и Софьи.
• А Софья получила 2 лайка от Алены и 1 от Варвары.

Царь взял лайки, покрутил гайки, постучал по колесам, пошмыгал носом, причмокнул губами, поскрипел зубами, сгонял в палаты и объявил результаты.

Наибольший вес лайков (7 баллов) получила Софья, но титул «мисс Салтан» достался Алене (15 баллов).


После объявления результатов девицы бросились обратились к царю с просьбой рассказать,- откуда взялись эти странные цифры?

На той неделе пришлось разбираться в логике работы одного бесплатного тула. Почти детективная история вышла с ее автором, который впоследствии оказался индусом канадского происхождения проживающим в Южной Америке.

Конечно же, практическая ценность была не в биографии автора, а в запросах, которые отправлялись приложением на сервер.

Установил. Запустил. Стал в стоечку и начал собирать профайлером все, чем приложение должно было «порадовать» сервер. Смею разочаровать – ничего радостного сервер в ближайшие два часа не увидел. В основном встречались разного рода перлы в запросах, которые явно не претендовали на комплименты:

SELECT
    LogTruncations = (
        SELECT TOP 1 SUM(cntr_value)
        FROM ##tbl_cnt
        WHERE counter_name = 'Log Truncations'
    ),
    LogShrinks = (
        SELECT TOP 1 SUM(cntr_value)
        FROM ##tbl_cnt
        WHERE counter_name = 'Log Shrinks'
    ),
    LogGrowths = (
        SELECT TOP 1 SUM(cntr_value)
        FROM ##tbl_cnt
        WHERE counter_name = 'Log Growths'
    ),
    ...

Поскольку их можно написать на порядок проще и сократить логические чтения из таблицы:

SELECT
    LogTruncations = SUM(CASE WHEN counter_name = 'Log Truncations' THEN cntr_value END),
    LogShrinks = SUM(CASE WHEN counter_name = 'Log Shrinks' THEN cntr_value END),
    LogGrowths = SUM(CASE WHEN counter_name = 'Log Growths' THEN cntr_value END),
    ...
FROM ##tbl_cnt

На этом можно было бы и закончить… Но практически под конец я увидел, что приложение вызывает пользовательские хранимые процедуры из tempdb. Поймал себя на мысли: «Когда приложение успело их создать… и главное зачем?»

В этой статье мы поговорим о проектировании архитектуры и создании мобильного приложения на основе паттерна MVP с использованием RxJava и Retrofit. Тема получилась довольно большой, поэтому подаваться будет отдельными порциями: в первой мы проектируем и создаем приложение, во второй занимаемся DI с помощью Dagger 2 и пишем тесты unit тесты, в третьей дописываем интеграционные и функциональные тесты, а также размышляем о TDD в реалиях Android разработки.

В первой части статьи мы разработали приложение для работы с github, состоящее из двух экранов, разделенное по слоям с применением паттерна MVP. Мы использовали RxJava для упрощения взаимодействия с сервером и две модели данных для разных слоев. Во второй части мы внедрим Dagger 2, напишем unit тесты, посмотрим на MockWebServer, JaCoCo и Robolectric.

Недавно мне попалась задачка на поиск почти-дублей среди большого количества коротких текстов. Поиск готового решения не привел к успеху, а полученное решение оказалось довольно интересным, и я не смог отказать себе в удовольствии поделиться им.

Формулировка

Есть большая база текстов (сотни тысяч текстов). Длины текстов примерно одинаковые, около 250 символов, язык — английский. Некоторые из текстов отредактированы (исправлены опечатки, расставлены запятые и т.п.); таким образом в базе оказывается как оригинальный текст, так и его исправленная копия. Таких пар не очень много, скажем не более 1%. Задача: найти все такие пары.

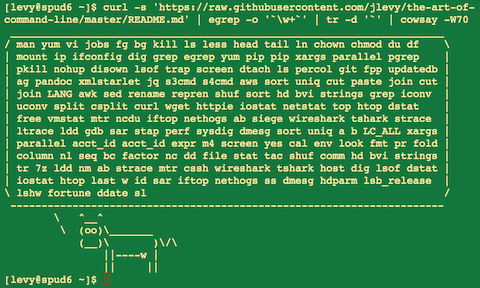
Вот уже как неделю английская версия the art of command line висит в секции trending на Github. Для себя я нашел этот материал невероятно полезным и решил помочь сообществу его переводом на русский язык. В переводе наверняка есть несколько недоработок, поэтому милости прошу слать пулл-реквесты мне сюда или автору оригинальной работы Joshua Levy вот сюда. (Если PR отправите мне, то я после того, как пересмотрю изменения отправлю их в мастер-бранч Джоша). Отдельное спасибо jtraub за помощь и исправление опечаток.

Содержание

1. Что такое тензор и для чего он нужен?
2. Векторные и тензорные операции. Ранги тензоров
3. Криволинейные координаты
4. Динамика точки в тензорном изложении
5. Действия над тензорами и некоторые другие теоретические вопросы
6. Кинематика свободного твердого тела. Природа угловой скорости
7. Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
8. О свертках тензора Леви-Чивиты
9. Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
10. Получаем вектор угловой скорости. Работаем над недочетами
11. Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
12. Параметры Родрига-Гамильтона в кинематике твердого тела
13. СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
14. Нестандартное введение в динамику твердого тела
15. Движение несвободного твердого тела
16. Свойства тензора инерции твердого тела
17. Зарисовка о гайке Джанибекова
18. Математическое моделирование эффекта Джанибекова

Введение

Это было очень давно, когда я учился классе в десятом. Среди довольно скудного в научном плане фонда районной библиотеки мне попалась книга — Угаров В. А. «Специальная теория относительности». Эта тема интересовала меня в то время, но информации школьных учебников и справочников было явно недостаточно.

Однако, книгу эту я читать не смог, по той причине, что большинство уравнений представлялись там в виде тензорных соотношений. Позже, в университете, программа подготовки по моей специальности не предусматривала изучение тензорного исчисления, хотя малопонятный термин «тензор» всплывал довольно часто в некоторых специальных курсах. Например, было жутко непонятно, почему матрица, содержащая моменты инерции твердого тела гордо именуется тензором инерции.

Меня давно занимал вопрос: «а что, если попробовать прогнать цифровую запись песни через преобразование Фурье, посмотреть зависимость спектра от времени и попытаться вытащить из полученной информации аккорды песни?». Вот, наконец, нашел время попробовать…

Здравствуйте, Хабравчане!
При работе с 2D графикой в Android отрисовку можно выполнять используя Canvas. Проще всего это сделать с помощью своего класса, унаследованного от View. Необходимо просто описать метод onDraw(), и использовать предоставленный в качестве параметра canvas для выполнения всех необходимых действий. Однако этот подход имеет свои недостатки.