How to become an author
Search
Profile
Pull to refresh

Comments 76

Замена гексогональному игровому гриду.
Total votes 6: ↑6 and ↓0 +6
Не совсем. В гексагональной решётке у каждой ячейки по 6 соседей, а тут у коричневых ячеек — восемь.
This comment wasn’t rated yet 0
Понятно, что традиционная гексогональная арифметика работать не будет… Nav Mesh наверное заменит арифметическую координатную систему. Надо поразмыслить…
This comment wasn’t rated yet 0
Скорее для loopy: http://www.chiark.greenend.org.uk/~sgtatham/puzzles/js/loopy.html
This comment wasn’t rated yet 0
Подскажите, почему не подходит такой тип пятиугольников? Вроде в перечисленных такого нет:
image
Total votes 21: ↑20 and ↓1 +19
есть такой, первый вид
шестиугольник разрезанный пополам, по сути
Total votes 19: ↑19 and ↓0 +19
Тогда и шестой вариант, который светло-фиотлетовый, туда же.
This comment wasn’t rated yet 0
Не совсем так. У первого типа формула
D + E = 180
то-есть два прилежащих угла в сумме дают 180. У шестого типа формула
C + E = 180, A = 2C, a = b = e, c = d
то-есть, во-первых, сумму 180 градусов дают углы, лежащие через один, и, во-вторых, несколько других ништяков. Даже если это шестиугольник, разрезанный пополам, то разрезан он хитрее, чем в первом случае.
This comment wasn’t rated yet 0
потому что он не выпуклый
Total votes 31: ↑0 and ↓31 -31
Да, как раз первый тип с формулой «D + E = 180», что означает, что сумма двух последних углов равна 180 градусам.
Total votes 6: ↑6 and ↓0 +6
Ну что, круто, что учёные активно работают над формой кафельной плитки.
Total votes 12: ↑10 and ↓2 +8
Если учёные работают над тем, что сразу же можно применить на практике, разве это не показывает реальную пользу исследований?
Total votes 14: ↑14 and ↓0 +14
На самом деле, данная информация может быть полезной, например, для проектирования матриц фотоаппаратов.
Если кто не в курсе, большинство матриц выглядят так:
Total votes 8: ↑8 and ↓0 +8
UFO just landed and posted this here
Ну пятиугольники вряд ли, но это не значит, что это не надо исследовать.
Total votes 4: ↑4 and ↓0 +4
Если нужно расположить сенсели равномерно, их три типа, и нет проблем сделать их многогранными — оптимальны давно нам известные гексы.
Total votes 1: ↑1 and ↓0 +1
Кстати, именно так и располагались компоненты в «тёплых ламповых» масочных кинескопах:
Как-то так
image

This comment wasn’t rated yet 0
У вас картинка отклеилась. Вероятно, было что-то вроде этого:

image

Надо сказать, расположение отверстий маски и форма триад связана с расположением электронных пушек.
Такая «гексагональная» сетка — в случае, когда пушки треугольником стоят, дельтообразно (так, кстати, они в круглой горловине компактнее расположены).
А вот если маска щелевая или апертурная — пушки в линию (компланарны).

image
Total votes 3: ↑3 and ↓0 +3
В математике всегда такие забавные сенсации?)
Total votes 22: ↑5 and ↓17 -12
Не всегда. Есть такие, где нужно изучение темы несколько лет, что бы можно было со знанием дела разок улыбнуться.
Total votes 20: ↑18 and ↓2 +16
Нет, иногда они выглядят так 1, 2, 3, 4 (все 4 части — это одно доказательство ABC-гипотезы, которое проверяется на корректность уже >3 лет).
Total votes 2: ↑2 and ↓0 +2
Серьезно, а в практическом плане, что это дает? Какие применения?
Total votes 18: ↑5 and ↓13 -8
UFO just landed and posted this here
Уважаемый, вы пожалуйста держите при себе свои предположения и советы. Если я с чем-то несогласен, то пишу прямо, а в данном случае я реально интересуюсь как человек из смежной отрасли.
Total votes 25: ↑5 and ↓20 -15
Чисто теоретически, любое построенное замощение плоскости или пространства может оказаться структурой какого-нибудь нового материала. Стрельнет или нет — заранее неизвестно.
Total votes 5: ↑5 and ↓0 +5
UFO just landed and posted this here
UFO just landed and posted this here
Что именно вы имеете в виду? ABC-гипотезу или Задачу о покрытии плоскости?
Если первое, то её доказательство приведет к грандиозному скачку вперед в теории чисел, если второе, то как минимум нужно дорешать задачу до конца, неопределенность с пятиугольниками не позволяет закончить заниматься этой задачей.
Total votes 2: ↑2 and ↓0 +2
Читайте «Математический цветник» Гарднера, кого заинтересовали пятиугольники.
Total votes 2: ↑2 and ↓0 +2
Так в статье же написано — «50-летняя американская домохозяйка и любительница математики Марджори Райс».
Total votes 5: ↑3 and ↓2 +1
Гарднер про нее писал
Total votes 1: ↑1 and ↓0 +1
Так о том и речь. Зачем читать «Математический цветник», если ответ есть прямо в статье? Конечно, если кому интересны подробности — чем занимаются американские домохозяйки вместо работы по дому — то могут и почитать.
Total votes 5: ↑2 and ↓3 -1
Ваше право иметь такое мнение, но не хочу, чтобы из-за вашего ехидного комментария у читателей сложилось превратное мнение о книге. Я в свое время с удовольствием ознакомился с математическими выкладками, которые приводили к получению этих прямоугольников.
Total votes 3: ↑3 and ↓0 +3
Значит, я неправильно понял ваш комментарий. Вместо «если вас заинтересовали пятиугольники, то почитайте Гарднера» я прочитал «почитайте Гарднера — там написано, кого заинтересовали пятиугольники». А зачем его для этого читать — ведь в статье все перечислены.
Total votes 6: ↑6 and ↓0 +6
Посмеялся, прочитав диалог вашим взглядом :) А я-то думал, что по вашему мнению, проблема пятиугольников не стоит внимания, раз только домохозяйки ей занимаются.
Total votes 3: ↑3 and ↓0 +3
В некоторых вариантах вижу мухлёж, потому что отражение — не настоящая линейная трансформация.

Если кому не понятно: берём плитку с красивой (одной) поверхностью заданной формы и обнаруживаем, что часть плитки надо перевернуть на «некрасивую» поверхность.
Total votes 10: ↑9 and ↓1 +8
В найденном варианте такой же мухлеж :)
Total votes 3: ↑3 and ↓0 +3
Почему же отражение — не лийнейная трансформация, если оно сохраняет сложение и умножение на скаляр?
This comment wasn’t rated yet 0
Я уже объяснил. В отличие от поворота и сдвига, «переворот» неявно подразумевает, что обратная сторона имеет такие же свойства, что и лицевая. А пример с кафелем отлично показывает, что это предположение слишком требовательно — у кафеля обычно зад некрасивый и предназначен для прилипания, в отличие от гладенькой лицевой поверхности.

Отражает ли мат.модель реальность или нет — вопрос второй. С бытовой точки зрения поворот и сдвиг — простые линейные операции. Переворот и масштабирование — очевидно нет, так как требуют отдельных кафелин.
Total votes 2: ↑2 and ↓0 +2
Интересно, какой из 15 вариантов используется на фотографии с плиткой? Такого паркета на рисунках нет.
Total votes 1: ↑1 and ↓0 +1
Я так понял на фотографии с плиткой пятиугольники двух разных типов: более острые и более тупые.
Total votes 1: ↑0 and ↓1 -1
Скорее всего, это частный случай 5-го варианта (тёмно-фиолетового), когда ещё один угол равен 120 гр, и ещё для одной пары сторон нужно равенство. Тогда 5-угольник попадает ещё и в первый тип. Так что нового там — только нетривиальный паркет.
This comment wasn’t rated yet 0
Сходил по ссылке. Это Type 3: A = C = D = 120, a = b, d = c + e
This comment wasn’t rated yet 0
Это вряд ли. Здесь A=D=2*B=120, a=b=c, d=e. И ещё неизвестно, есть ли ограничения на C и E.
This comment wasn’t rated yet 0
Как это так один и тот же пятиугольник может подпадать под два разных варианта?
Если бы так могло быть, то разве не был бы один из этих двух вариантов просто частным случаем другого варианта?
This comment wasn’t rated yet 0
Точно так же, как квадрат является частным случаем и прямоугольника, и ромба. При этом ни ромбы в целом не являются частными случаями прямоугольников, ни наоборот.
Total votes 1: ↑1 and ↓0 +1
«Мы открыли фигуру с помощью компьютерного перебора большого, но ограниченного количества вариантов, — говорит Кейси Манн

Получается сбрутфорсили?
Total votes 3: ↑2 and ↓1 +1
Вы так говорите, как будто это что-то плохое.
Total votes 8: ↑8 and ↓0 +8
Плитка красивая, а среди 14-ти вариантов по ссылке ее похоже нет.
This comment wasn’t rated yet 0
Потому что, цитирую,

> Это… 15-й вид таких пятиугольников…
Total votes 8: ↑5 and ↓3 +2
Я имел в виду плитку на последней картинке в посте. 15-й вид это 1-я трехцветная картинка, как я понял, в середине 14 известных ранее вариантов и плитки с последней картинки среди них нет или она получается из одного из 14-ти вариантов, но сколько не смотрел не получается понять из какого и как.
This comment wasn’t rated yet 0
Был интересный подкаст «Наука 2.0» с Валентином Крапошиным о квазикристалах пятого порядка. Там интересно о том, что пятиугольники на самом деле − это лучший способ «захватывать» пространство. Рекомендую.
Total votes 1: ↑1 and ↓0 +1
Так вот, оказывается, чем они там в Пентагоне занимаются.
Total votes 4: ↑4 and ↓0 +4
Шестнадцатым предлагаю пятиугольник, у которого один угол равен 180°, а остальные 4 — 90°.
Total votes 14: ↑9 and ↓5 +4
Без пояснительных рисунков, объяснений того, что из себя представляет угол в 180°, и прямого указания на то, что не надо все настолько серьезно воспринимать, видимо, посетители GT не способны оценить комментарий. Сейчас еще и выяснится, что предыдущее предложение оказалось слишком сложным для них.
Total votes 1: ↑1 and ↓0 +1
Он входит в первый тип
This comment wasn’t rated yet 0
Сомневаюсь. Там распиленные пополам гексагоны, у них никак четыре угла по 90° не получатся.
This comment wasn’t rated yet 0
Получатся. Надо брать центрально-симметричные 6-угольники с углами 90, 90, 180, 90, 90, 180 и резать их пополам, соединяя середины сторон, углы на концах которых по 90 гр. Получится два ваших пятиугольника.
Total votes 4: ↑4 and ↓0 +4
Хм, действительно. Ошибки случаются.
Total votes 1: ↑1 and ↓0 +1
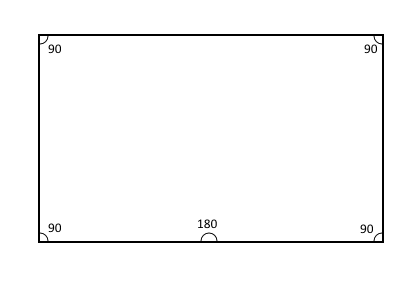
Type 3 пятиугольники так близки к красивой симметричной форме, и из-за этого смотреть на них перфекционисту ещё больнее.
Ну немножко выровнять углы разреза, ну!
image
Total votes 4: ↑4 and ↓0 +4
Да это ж соты! Просто с перекрестием внутри.
This comment wasn’t rated yet 0
Ну так и в оригинале тоже соты, просто НЕРОВНЫЕ.
This comment wasn’t rated yet 0
Там и первый вариант — тоже шестиугольники, только на две части разрезанные. И тоже можно было сделать более наглядно, но, видимо, целью было наоборот скрыть простоту решения. Не знаю, зачем.
Total votes 2: ↑2 and ↓0 +2
Целью было показать наиболее общие варианты — с возможно более неправильными углами и неравными сторонами. Чтобы читатель не подумал, что, например, в 3-м варианте пятиугольники обязательно должны быть симметричными.
Total votes 2: ↑2 and ↓0 +2
Ежели я правильно понимаю, то именно в третьем случае (а также в большинстве остальных) форму пятиугольников изменить (с сохранением замощения) никак не получится.
This comment wasn’t rated yet 0
Судя по формулам, приведённым по ссылке, свобода есть во всех 14 случаях — там нет даже ни одного варианта с фиксированными углами. В третьем варианте заданы углы A,C и D, но B можно выбирать любым (E=180-B). Так что одна степень свободы есть — ориентация лучей разреза относительно шестиугольника.
This comment wasn’t rated yet 0
Возможно, пятиугольники, покрывающие плоскость, могут найти применение в картографии. Для отображения на плоскости участков поверхности Земли, Луны, Марса и т.п. Но сначала надо разметить поверхность космического объекта соответствующе трансформированными выпуклыми пятиугольниками (с несколько иными значениями углов), чтобы они покрывали выпуклую поверхность космического объекта. Вероятно, пятиугольники лучше подойдут для отражения динамики поверхности космического объекта — тектонические процессы «текут» в некоторых направлениях и вытянутое направление пятиугольника может оказаться более адекватным, чем правильный, или даже лучше чем вытянутый шестиугольник.
This comment wasn’t rated yet 0
Треугольники, тем более, рекурсивно делящиеся, подойдут для этого еще лучше.
This comment wasn’t rated yet 0
Согласен. Любой пятиугольник можно разделить на некоторое множество треугольников. Это множество треугольников будет фракталом треугольников в пятиугольной матрице, множество пятиугольников в свою очередь будет классом пятиугольного фрактала.
This comment wasn’t rated yet 0
Only those users with full accounts are able to leave comments. Log in, please.

Your account

Sections

Information

Services

Support
© 2006–2023, Habr