Алгоритмы *

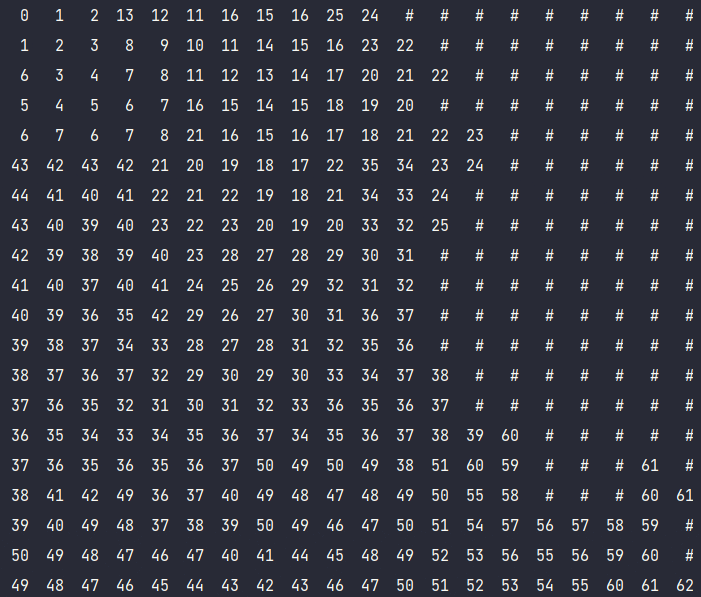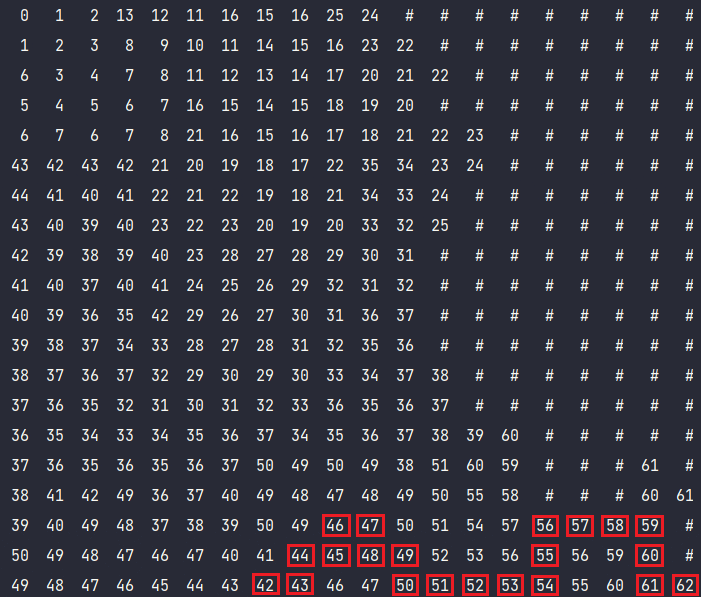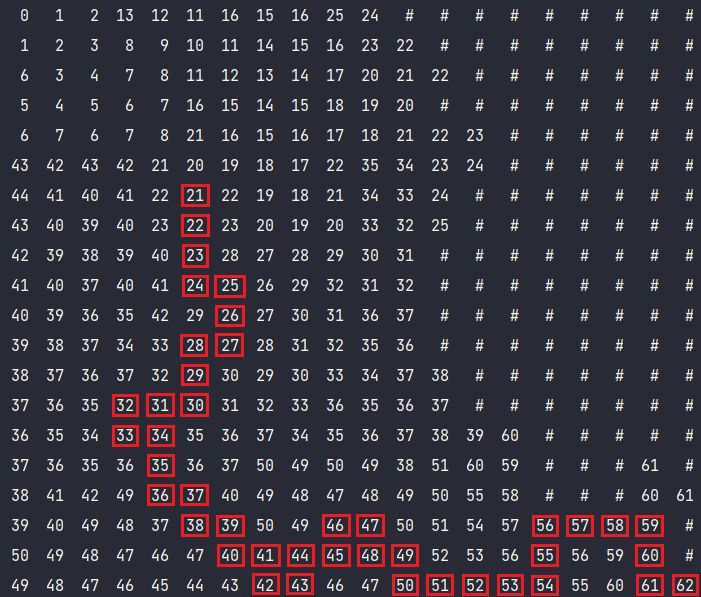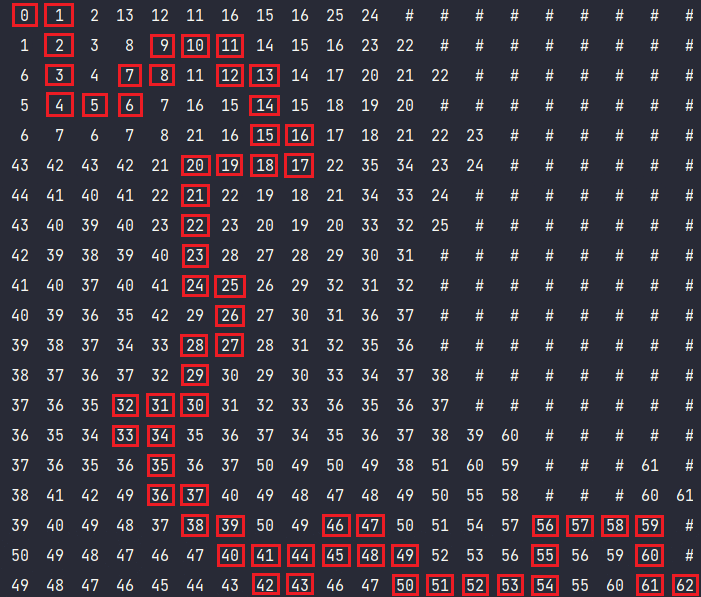
Волновой алгоритм — алгоритм поиска пути, алгоритм поиска кратчайшего пути. Принадлежит к алгоритмам, основанным на методах поиска в ширину.

В предыдущей статье мы рассмотрели сложность некоторых игр и головоломок. Данная тема вызвала некоторый интерес, вот и продолжение. В комментариях некоторые читатели высказали свои пожелания, которые я постарался учесть.

В первой статье и правда по справедливому замечанию avsmal «не хватает каких-то более строгих и конкретных утверждений», но не стоит забывать, что любой даже самый нудный материал нужно стараться подать интересно. В прошлый раз я пожертвовал структурой и конкретностью в пользу читабельности и привлечения интереса к теме. Сильно «душные» статьи заходят с большим скрипом и больше отпугивают читателя.

Прежде всего, нужно отметить, что теория вычислительной сложности анализирует сложность различных алгоритмических задач, а теория вычислимости — какие проблемы могут быть решены с помощью алгоритмов. Теория сложности рассматривает проблемы, которые в принципе могут быть решены алгоритмически, и пытается установить экстремумы ресурсов, необходимых для их решения. Это важно, потому что некоторые проблемы в принципе могут быть решаемы, но требовать неосуществимого количества ресурсов.

Александр Пряхин, руководитель разработки юнита в Авито Работа, рассказал, так ли мрачно выглядит будущее для разработчиков «из плоти и крови» на фоне активного развития No Code, Low Code и нейросетей.

Каждый из нас из школы помнит определение Евклидова расстояния между двумя точками на плоскости. С помощью расстояния Евклида можно вычислить расстояние между двумя точками на карте, например, между вашим местоположением и станцией метро. Но для пешехода в Нью-Йорке расстояние между двумя точками в городе будет отличаться от расстояния Евклида между двумя точками из-за невозможности передвигаться иначе, как по проезжим улицам, пересекающимся под прямыми углами. Такое расстояние так и называется: "расстояние городских кварталов" или манхэттенское расстояние. При любом способе расстояние характеризует меру близости точек. В сегодняшней статье мы расскажем о способах вычисления расстояния между двумя словами.

Наши убеждения и представления могут ограничивать наши возможности, но у любопытства нет границ даже там, где начинается полная неизвестность.

Ресурсы

• Build Your Own Text Editor — наверно, самый фундаментальный пост о создании текстового редактора с нуля, который я видел. Это превосходный туториал на случай, если вы хотите начать писать собственный текстовый редактор. Стоит заметить, что в редакторе из этого туториала в качестве внутренней структуры для текста используется, по сути, вектор строк.
• Text Editor: Data Structures — отличный обзор множества структур данных, которые можно использовать при реализации текстового редактора. (Спойлер: как минимум одна из них будет рассмотрена в моём посте)
• Плейлист Ded (Text Editor) на YouTube — это потрясающая серия, в которой @tscoding фиксирует процесс создания с нуля текстового редактора. Эти видео стали для меня источником вдохновения.

Зачем?

1. Я хотел заняться проектом, непохожим ни на один свой прошлый.
2. Я хотел создать инструмент, которым смогу пользоваться.
3. Мне всегда хотелось глубже разобраться с созданием собственных структур данных.

Играясь с генерацией карт высот в unity, я заметил одну неприятную тенденцию: большинство статей и материалов рассказывают либо о Value Noise, либо о Perlin Noise, либо о Voronoi Noise. Возможно я плохо искал, но это не отменяет того факта, что я сел писать эту статью, поэтому для всех нуждающихся я сделал шпаргалку.

Под этим термином понимаются такие структуры данных или алгоритмы, результатом которых является не детерминированное «да» или «нет», а вероятностные ответы, например, «точно нет» и «возможно». Как правило, такие структуры позволяют существенно сэкономить вычислительные ресурсы в задачах, где допустимо получить примерный ответ.

В этой статье я сделаю обзор таких структур данных и расскажу, какую пользу они могут принести на практике. К базовым вероятностным структурам данных можно отнести фильтр Блума, HyperLogLog и Count-Min Sketch.

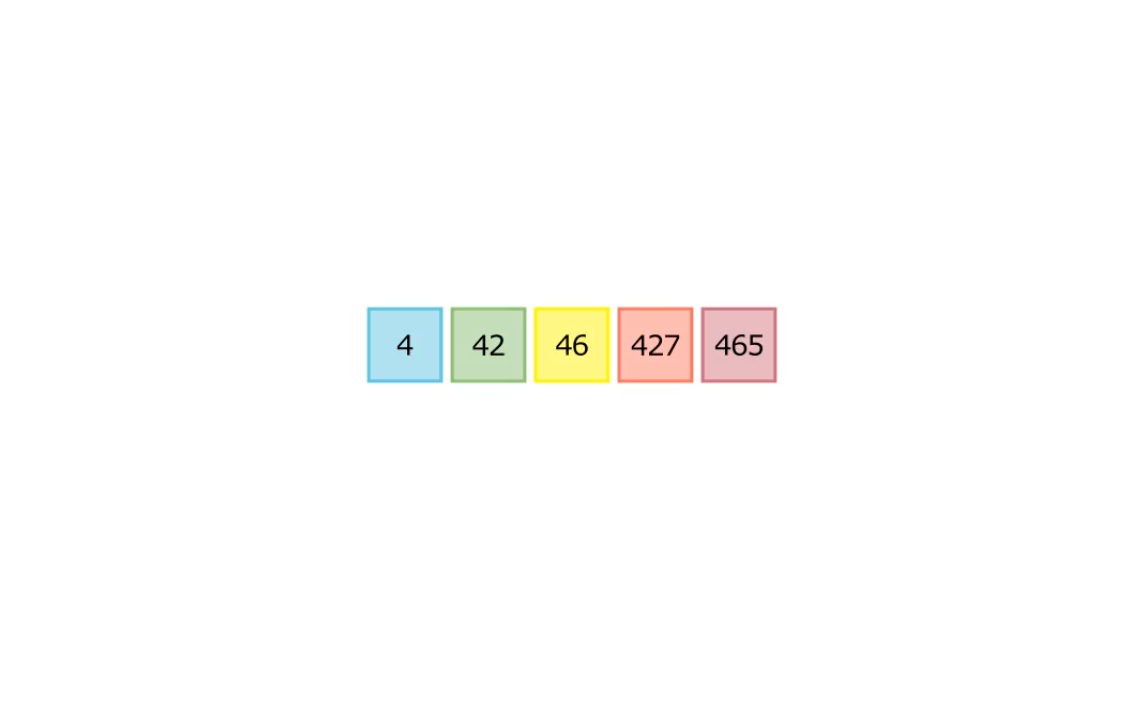
Чему равно самое большое число, которое можно составить из этих пяти карточек? И как написать программу, которая быстро найдёт ответ, получив на вход сто таких карточек?

Данная публикация служит пояснительным материалом к предыдущей, а так-же самостоятельной для тех, кто читает по данной теме мои публикации впервые.

Сначала о том, каким алгоритмом я планирую заменить в своих работах свёрточные нейросети. Чтобы это работало быстро - нужны карты трассировок. Линии трассировок на карте расположены параллельно под определённым углом на каждой карте - так и происходит условная поляризация. Генератор карт работает быстро и генерирует он карты трассировок направленных прямыми линиями, обрыв каждой линии он отмечает в данных. То-есть сначала запускатеся генератор карт и генерирует картинку, данная анимация существенно отличается от работы генератора и показывает только его ТЗ - в каждом пикселе карты записать координаты следующего пиксела и обозначить в данных окончание каждой линии. Изображения я взял небольшие, но тем не менее файлы анимации достаточно увесистые. Допустим что обрабатываемые изображения будет 7*7 пикселов, а карт трассировок всего четыре, тогда ТЗ генератора примерно будет выглядеть так, но на самом деле его алгоритм намного сложнее и работает на много быстрее - он ничего практически не считает и выдает большие объёмы данных автоматически, но об этом позже, а пока так чисто визуально

Транслятор Expression'ов в GraphQL-запрос.

Реализация библиотеки для трансляции Выражений в GraphQL-запрос с использованием Linq-подобного api.

Обзор и сравнение существующих решений. Создание собственного инструмента.

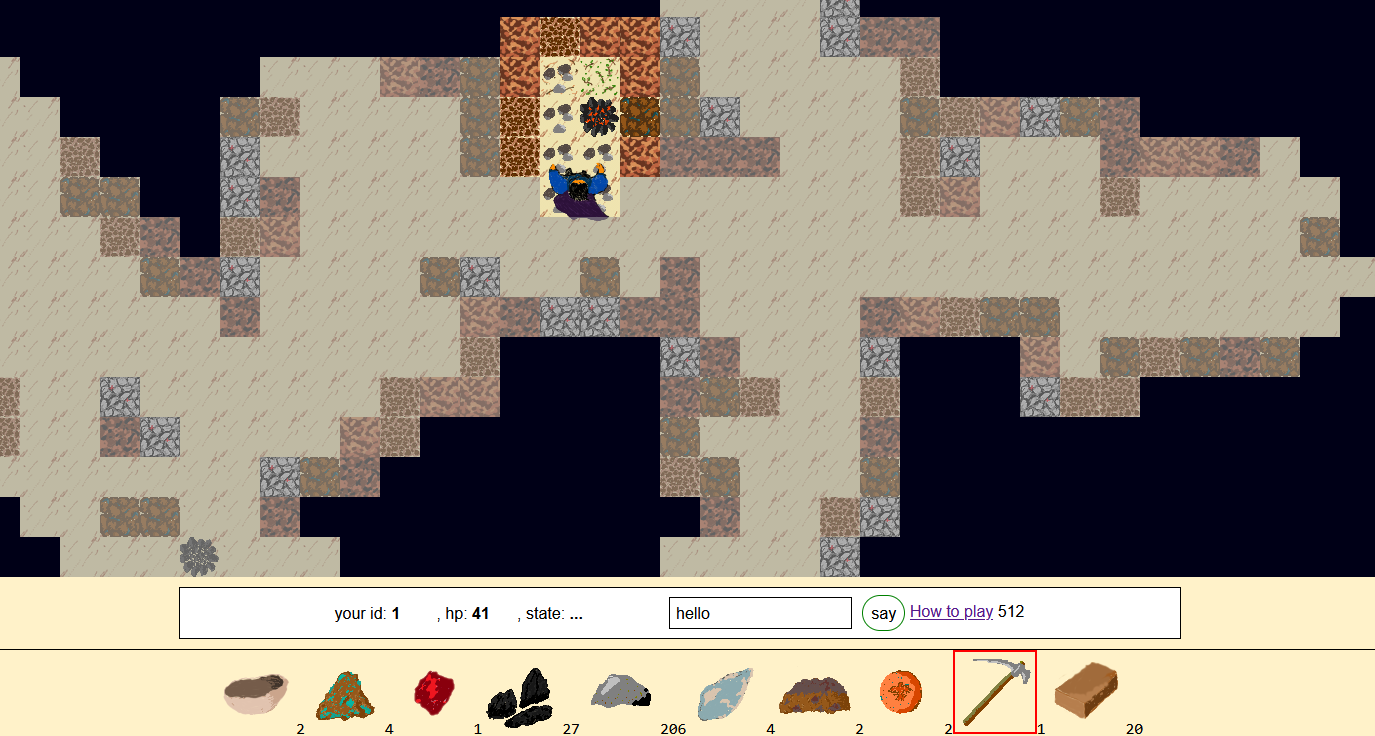
Когда-то давно меня очаровал ADOM. Я даже и близко не подошёл к прохождению игры, но мне нравилось бродить по этому миру, собирать предметы с эффектом, который не прочувствуешь, пока не используешь. Нравилось, что монстры в подземельях имели какие-то зачатки собственного интеллекта, подбирали с пола вещи и использовали их. Всё время что-то происходило и менялось, проходишь по тому же месту – смотришь кто-то уже подобрал с пола монеты. Или предметы в инвентаре испортились. Мир как будто живёт своей жизнью. В пещерах можно идти по коридорам, а можно наугад пробивать туннели заклинанием в надежде отыскать потайную комнату, оставляя на полу груду камней. Мир полный возможностей и способов взаимодействия.

Вдохновившись этими впечатлениями, я задумался, а может можно сделать что-нибудь своё, пропитанное подобным духом? И почему бы не попробовать сделать многопользовательскую игру с современной то скоростью интернета? Ведь это даёт особые ощущения, осознание того, что ты идёшь по туннелю, вырытому другим, настоящим, игроком. Или вот-вот встретишь его за углом.

Недавно Youtube (*сайт, нарушающий закон РФ) порекомендовал мне любопытный с различных сторон видеоролик. В нём рассматривалась задача, которую, по словам автора, задают на собеседовании при приёме на работу в Apple.

Изобретение машины Тьюринга в 1936 году Аланом Тьюрингом положило начало современным вычислениям.

В 1928 году немецкие математики Давид Гильберт и Вильгельм Аккерманн предложили вопрос, названный Entscheidungsproblem («проблема принятия решения»). Со временем их вопрос привёл к формальному определению вычислимости, которое позволило математикам ответить на множество новых проблем и заложило основу теоретической информатики.

Определение пришло от 23-летнего аспиранта по имени Алан Тьюринг, в 1936 году написавшего основополагающую статью, которая не только формализовала концепцию вычислений, но и доказала фундаментальный вопрос математики и заложила интеллектуальную основу для изобретения вычислительной техники.

Привет, Хабр!

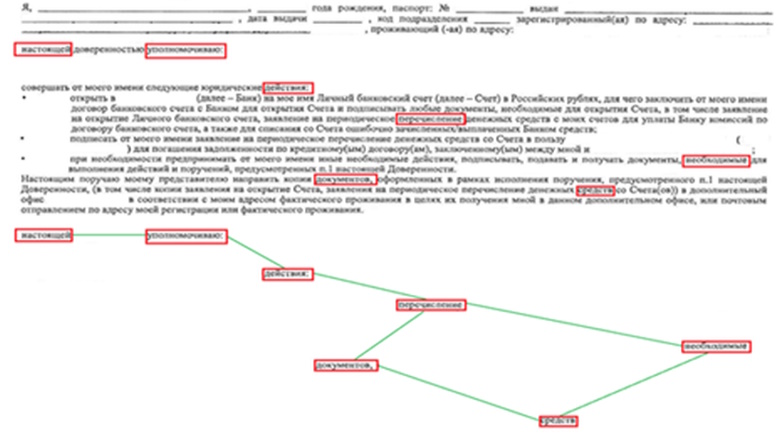
В сегодняшней статье будет рассмотрен анализ структуры деловых документов. Деловой документ предназначен для обмена данными между организациями и физическими лицами. Деловые документы характеризуются относительно простой структурой и ограниченным словарем статических текстов. Объемы потоков входящих и исходящих бумажных документов в крупных организациях могут достигать нескольких миллионов страниц в день, поэтому ручная обработка большого потока документов невозможна. Анализ текста и распознавание документа – известные задачи, однако анализ распознанного документа имеет свои особенности, о которых мы далее расскажем.

С прошлой осени Нивен проходит стажировку, разрабатывая новую модель псевдонимов для Rust: древовидные заимствования (tree borrows). Секундочку, уже слышу, как вы вопрошаете: а разве в Rust ещё нет своей псевдонимной модели? Разве вы, автор, не рассказываете повсюду о «стековых заимствованиях»? Действительно, так и есть, но стековые заимствования — всего лишь один из возможных вариантов реализации для модели псевдонимов, и с этим вариантом есть свои проблемы. Древовидные заимствования призваны учесть опыт, усвоенный при работе со стековыми заимствованиями, и построить новую модель, не такую проблемную. Также при её проектировании принимаются немного иные решения, с учётом некоторых нужных компромиссов и той тонкой настройки, которая, возможно, должна быть привнесена в эти модели, и только потом настанет время решать, какую же из этих моделей принять в Rust в качестве официальной.

У себя в блоге Нивен написал подробное введение в древовидные заимствования, и не помешает сначала прочитать этот ознакомительный материал. На прошедшей недавно конференции RFMIG он выступил с лекцией на эту тему, и его доклад вы также можете посмотреть, вот здесь. В этом посте я сосредоточусь на том, чем древовидные заимствования отличаются от стековых. Предполагаю, что вы уже ориентируетесь в стековых заимствованиях и хотите понять, что меняется с введением древовидных заимствований.

Для краткости я буду иногда называть стековые заимствования «СЗ», а древовидные заимствования — «ДЗ».

В этой статье продолжим тему решения криптографических задач с ресурса MysteryTwister. И сегодня на очереди любопытный шифр, далёким предком которого является квадрат Полибия. Мы познакомимся с трёхраздельным шифром Феликса Деластеля. Что интересно информации об этом энтузиасте  криптографии очень мало в английском и французском сегментах сети (Деластель — француз), а в русскоязычном о нём почти нет совсем, хотя наверняка человеком он был очень неординарным. Почему я так решил? Да потому, что Феликс Деластель по роду профессиональной деятельности не имел к криптографии совершенно никакого отношения, поскольку всю жизнь проработал в порту Сен-Мало и криптографией занимался факультативно. Тогда как ранее и позже криптография была уделом учёных, профессиональных военных и дипломатов. Биографических данных о нём очень мало, но одно известно точно: на рубеже XIX и XX веков Деластель написал книгу "Traite Elementaire de Cryptographie" (Базовый трактат по криптографии), в которой он описывал системы шифрования, которые создал.

Всем доброго времени суток!

Эта коротенькая заметка посвящена симпатичной задачке генерации в лексикографическом порядке всех правильных скобочных последовательностей. Её нередко включают в список задач для подготовки к собеседованию (например, здесь).

По просторам инета гуляет следующее решение:

Привет, Хабр!

Недавно друзья задали мне задачу из дискретной математики, которой я хочу с вами поделиться.