Параллельное программирование *

Это перевод первой главы из поста How Async/Await Really Works in C#

Этот пост .Net блога является продолжением исходного поста, глубоко погружающим в историю, приведшую к созданию конструкций async/await и стоящие за этим дизайнерские решения и детали реализации async/await в C# и .NET.

Исходный пост What is .NET, and why should you choose it? предоставляет обзор платформы на высоком-уровне, перечисляя различные компоненты и решения на уровне дизайна, и предваряя последующие посты в глубину обозначенных тем.

Ссылки в развитие темы:

1. Часть 2 Артефакты от EAP шаблона, SynchronizationContext

2. Уроки по асинхронному программированию из первой половины работы

3. Параллельные вычисления — Все дело в контексте-синхронизации (SynchronizationContext)

4. Async/Await из C#. Головоломка для разработчиков компилятора и для нас

Упомянутая в заглавии книга (далее H&H) - это про железо [15]. Я - про программирование, но на базе "железной модели" конечного автомата. И там и там математическая основа одна. Все это, действительно, крутая железная концепция, помогающая поставить не только синтез цифровых схем, но и программирование на совершенно другие рельсы, определяющие его будущее.

Параллелизм у программистов нынче в моде. Но, видимо, они (программисты) совсем не в курсе, что разработчики железа давным-давно погружены в эту тему. А потому им (я все про программистов) есть у кого поучиться. Но, похоже, некие амбиции-заскоки этому  мешают. Но, если вы этим не страдаете, то прочитайте книгу H&H и дойдите, ну, хотя бы до 4-й главы. Попробуйте реализовать одно-два упражнения, используя свой, программистский инструментарий - всякие там корутины, потоки и весь сопутствующий этому террариум. Убедитесь в его полном бессилии. И тогда, может, это заставит кое-что пересмотреть, переосмыслить. Только представьте: логический элемент - отдельный процесс, десятки, сотни, тысячи элементов - множество параллельных процессов, и все это в вашей ладошке (это я про смартфон) и даже работает!

Но пришло время исполнять обещанное (см. предыдущую часть темы в [1]). И пусть количество "плюсов" пока не достигло заданной планки, но ... если каждый "минус" считать за два "плюса", то это уже более чем ... ;) Так что спасибо всем, давшим положительную оценку - нет, не автору, а затронутой теме. Области знаний, от которой многое сейчас зависит.  Это те слова, которые мы вправе сказать в адрес теории, посвященной  синтезу цифровых схем, в адрес тех, кто занимался и занимается ее развитием, становлением и внедрением в практику.

Как правильно использовать возможности параллельного программирования?
Зачем программистам математика и зачем знать алгоритмы?

На примере небольшой задачи мы вместе ответим на эти вопросы. А так же хочу наглядно продемонстрировать преимущества создания однородных задач.

Весь код из статьи находится здесь.

Всем привет! В этой статье я бы хотел погрузить в мир жизненного цикла потоков начинающих программистов на Java, заранее извиняюсь за злоупотребление слова "поток" в этой статье, но я надеюсь так будет даже лучше для понимания. Поехали!

Жизненный цикл потока - основная концепция Java, которую мы подробно рассмотрим в этой статье. Мы будем использовать краткую иллюстрированную диаграмму и фрагменты практического кода, чтобы более глубоко понять состояния потока во время его выполнения. Эта статья о создании потока - отличное начало для понимания потоков в Java.

Привет, Хабр! В этой статье я хотел бы поделиться опытом создания своего языка программирования.

Предыстория

Мне 14. Обучаясь на втором году Яндекс Лицея, нужно было написать несколько проектов. Первым из них стал проект на PyQT5. Я долго думал над идеей и вспомнил, что летом я хотел создать свой язык, но у меня этого не получилось (Тогда я не понимал как работает парсер и абстрактное синтаксическое дерево, поэтому забросил). И вот, мне пришла идея - сделать свой язык программирования и написать для него IDLE (т.к. тема проекта все таки QT). Ещё полгода назад я изучал асинхронность и многопоточность, поэтому именно одну из этих идей я хотел воплотить в своём языке. В данной статье я хотел рассказать устройство интерпретируемых языков и как их создать.

В этой статье мы обсудим паттерн "Cancellation Token", популярный в некоторых других языках, но почему-то обойденный вниманием в Python-сообществе. Он о том, как безопасно и красиво завершать работу функции, треда или корутины.

В предыдущей публикации Фортран: пишем параллельные программы для суперкомпьютера мы рассмотрели общий подход к программированию в массивно-паралллельной архитектуре (MPP) с использованием языка Фортран-2018 и дали пример запуска массивно-параллельной программы на одной машине с многоядерным процессором. В настоящей статье мы рассмотрим запуск массивно-параллельных программ на кластере высокой производительности (HPC) или кластере высокой готовности (HA). Код в данной статье пишется на языке Фортран-2018 с использованием комассивов (coarrays) и преобразуется компилятором Фортрана в вызовы фреймворка MPI.

Несколько лет назад я прочитал статью о параллелизации в GO и ничего не понял – я тогда только начинал программировать на этом языке. Но размышления автора мне очень понравились – они подкреплялись бэнчмарками, что было довольно убедительно. Автор игрался c параметром GOMAXPROCS и показал, что увеличение этого параметра не всегда приводит к увеличению производительности. Под конец статьи он подобрал такое значение, которое будет максимально эффективным для его функции, на мое удивление, это значение оказалось равно единице! Т.е. его код работал максимально эффективно, если работал всего на одном ядре процессора! Однако, в одном из комментариев под той статьей я прочел, что все эти изыскания нелепы, поскольку та же самая функция из статьи запущенная всего в один поток оказывается эффективнее любой ее параллельной реализации.

С тех пор я написал уже много кода на GO, и могу поделиться мыслями о шаблонах параллельной обработки с теми, кто находится в том же состоянии, что и я когда то.

За то время что я занимаюсь менторством я заметил, что большинство вопросов новичков связаны с темами: конкурентность, параллелизм, асинхронность. Подобные вопросы часто задают на собеседованиях, в работе эти знания позволяют писать более эффективные и производительные системы.

Цель статьи - понятно и доходчиво, используя примеры кода и бенчмарки рассказать о том какие инструменты есть в Python и как с их помощью добиться высокой производительности.

"Зацепила" крайняя статья про многопоточность [1]. Но, с другой стороны, - а что ожидал автор, предложив исходное решение без синхронизации? Получил то, что и должен был получить. На другое рассчитывать было бы достаточно наивно. Во-первых, потому, что используется весьма  проблемная модель параллелизма. Во-вторых, расплывчатое представление о решаемой проблеме (по крайней мере, если судить по описанию). Но это уже мое личное мнение и хотелось бы его пояснить. И не просто так, а подкрепив решением.

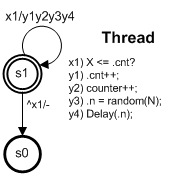
Имеем счетчик. Только это уже не просто счетчик, а общий ресурс, с которому пытаются получить доступ множество параллельных процессов. Налицо некая общая проблема, с которой приходится сталкиваться на практике. Тут можно добавить, что проблема эта давняя, рассматривалась не раз и ее решений предлагалось множество.

Но, может, автор достиг чего-то нового? Да, вроде, нет. То, что нужно синхронизировать - не новость. Нов ли предложенный механизм синхронизации? Не знаю, поскольку не специалист в  Python. Надеюсь такие найдутся и ответят на этот вопрос.

Покажу, как подобные проблемы решаю я. Причем совсем не прибегая ни к многопоточности, ни к всему тому, что нынче на волне успеха в так называемом параллельном программировании. И, как сказал автор статьи, "не спешите закрывать вкладку", а посмотрите, что будет дальше. А вдруг вам понравится?

Но для начала...

Краткая история вопроса

Использование переменной-счетчика в качестве общего ресурса - отнюдь не новость. Это элементарный и естественный подход к демонстрации проблем множества параллельных процессов. Насколько я припоминаю, впервые с подобным примером в серьезной литературе я столкнулся в книге [2].Предлагаемые там решения не вызвали восторга, а потому были задвинуты. И, кстати, об этом я не испытываю сожаления.

В данной статье я покажу на практическом примере как устроена многопоточность в Python, расскажу про потоки, примитивы синхронизации и о том зачем они нужны.

Изначально я планировал что это будет простая и короткая заметка, но пока готовил и тестировал код нашел интересный неочевидный момент связанных с внутренностями CPython, так что не спешите закрывать вкладку, даже если вы уверены что вы знаете о потоках в Python всё :)

Чтобы написать продолжение предыдущей статьи мне пришлось перечитать множество материалов, имеющих отношение к теме. Я так и не нашел пример хоть какой‑то практической задачи, определяющей хоть какие‑то детали, имеющие отношение к возможности распараллеливания. По большому счету все пишут о том, что распараллеливание улучшает производительность, и это в общем‑то все к чему нужно стремиться с невнятными оговорками о том, что при этом можно получить кучу проблем.

Но хуже того, что никто не рассматривает практических задач, для которых можно или нужно применять многопоточность никто не вспоминает что многопоточность придумали в те времена, когда никто не рассчитывал на то, что процессоры могут быть многоядерными.

Мне кажется нельзя считать что вы до конца понимаете концепцию многопоточности (Multithreading/ Concurrency) если вы не понимаете когда (для каких задач) ее можно и/или нужно использовать на однопроцессорной машине, 2-х процессорной, N‑процессорной машине и от чего это зависит.

Рассмотрим разницу между популярными ошибками при работе с многопоточностью, такими как Data Race и Race Condition, а также способами борьбы с ними.

Привет, Хабр! Я Артём Чаадаев из команды ассортимента размещения в Туту и занимаюсь разработкой на языке Go. Здесь мы посмотрим как решить распространенную практическую задачу применяя паттерны Semaphore и Worker Pool.

Хотите научиться конкуретной разработке на Go? Значит, вам сюда.

Добро пожаловать под кат!

Делая свой очередной пет-проект подумал, что мне нужна конкурентная очередь с приоритетами. Оказалось она была не нужна, но желание ее реализовать никуда не ушло.

Проведя небольшой поиск, нашел несколько научных статей с конкурентной реализацией и выбрал одну в качестве образцовой.

Потратив время и нервы на ее понимание и реализацию, был отрицательно удивлен результату: ее производительность хуже чем глобальная блокировка на всю структуру данных.

Здесь описал свою реализацию и сделал сравнение с блокирующей реализацией.
Критика (даже не конструктивная) приветствуется.

Создались условия, чтобы подвести некий итог. Дело в том, что автоматы в SimInTech  могут быть инерционными. И это определенно знаменательный факт. Более того, он даже радует своей неожиданностью, опровергая то фактическое неверие, которое к среде было до этого. Но давайте подробнее о том, как это все таки случилось...

Программисты, как правило, кушают то блюдо, которое им подают. Будь это язык программирования, библиотека, фреймворк или IDE. Однако, это еще полбеды. Удивляет нежелание выбирать. Хотя это тоже можно объяснить. Выбор‑то, может, и есть, сколько новых языков появилось за последнее время, но только разницы между ними особой нет. В результате, попробовав раз, попробовав два, мы устаем и останавливаемся на чем‑то одном, т. е. пресыщаемся...

Всем нам предстоит поддерживать уже существующий код, а также проводить ревью кода коллег.

Иногда становится очень тяжело видеть некоторые паттерны, которые кажутся безобидными, но при некорректном использовании или после неосторожного рефакторинга могут привести к различным проблемам: утечке горутин и каналов, повреждению целостности структур данных, паникам, трудноуловимым багам в бизнес-логике, самому страшному - неутолимому желанию порефакторить код, который выглядит как то, что вы бы написали в первый день работы с Go.

В своей статье я хочу дать рекомендации, которые, по моему мнению, могут помочь избежать перечисленных выше проблем.