Скачать статью в виде документа Mathematica (NB), CDF-файла или PDF.
Выражаю огромную благодарность
Кириллу Гузенко за помощь в переводе.
В этой статье систематически проверяются некоторые свойства фигуры, известной с древних времён, называемой
арбелос. Она включает в себя несколько новых открытий и обобщений, представленных автором данной работы.
Введение
Будучи мотивирован вычислительными преимуществами, которыми обладает
Mathematica, некоторое время назад я решил приступить к исследованию свойств арбелоса — весьма интересной геометрической фигуры. С тех пор я был впечатлен большим количеством удивительных открытий и вычислительных проблем, которые возникали из-за всё расширяющегося объёма литературы, касающейся этого примечательного объекта. Я вспоминаю его сходство с нижней частью культового велосипеда пенни-фартинг из The Prisoner (телесериал 1960-х), шутовской шапкой Панча (знаменитых Punch and Judy) и символом инь-ян с одной перевёрнутой дугой; см. рис. 1. В настоящее время существует специализированный каталог архимедовых кругов (круги, содержащиеся в арбелосе) [1] и важные применения свойств арбелоса, которые лежат вне поля математики и вычислительных наук [2].
Многие известные исследователи занимались этой темой, в том числе Архимед (убитый римским солдатом в 212 г. до н.э.), Папп (320 г. н.э.), Кристиан О. Мор (1835-1918), Виктор Тебо (1882-1960), Леон Банкофф (1908-1997), Мартин Гарднер (1914-2010). С недавних пор свойствами арбелоса занимаются Клейтон Додж, Питер Ай. Ву, Томас Шох, Хироши Окумура, Масаюки Ватанабе и прочие.
Леон Банкофф — человек, который привлекал всеобщее внимание к арбелосу в последние 30 лет. Шох привлёк внимание Бэнкоффа к арбелосу в 1979 году, открыв несколько новых архимедовых кругов. Он послал 20-страничную рукописную работу Мартину Гарднеру, который направил её Бэнкоффу, который затем отправил 10-страничный фрагмент копии рукописи Доджу в 1996 году. Из-за смерти Бэнкоффа запланированная совместная работа была прервана, пока Додж не сообщил о некоторых новых открытиях [3]. В 1999 году Додж сказал, что ему потребуется от пяти до десяти лет, чтобы отсортировать весь материал, которым он располагает, разложив всё это дело по стопкам. В настоящее время эта работа все ещё продолжается. Не удивительно, что в четвертом томе
The Art of Computer Programming, сказано о том, что важная работа требует большого количества времени.
 Рис. 1. Велосипед пенни-фартинг, куклы Панч и Джуди, физический арбелос.
Рис. 1. Велосипед пенни-фартинг, куклы Панч и Джуди, физический арбелос.
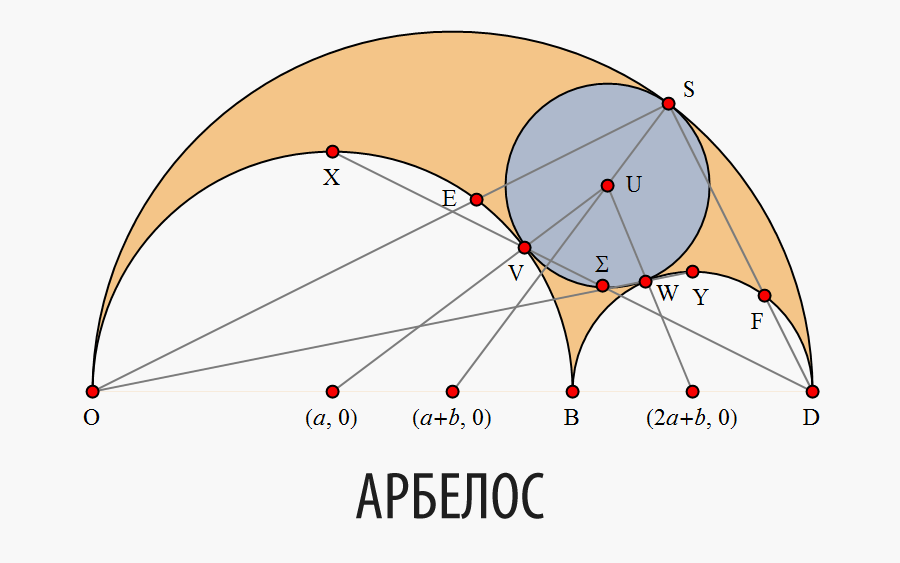
Арбелос (“нож сапожника” в греческом языке) назван так из-за своего сходства с лезвием ножа, использующегося сапожниками (Рис. 1). Арбелос — плоская область, ограниченная тремя полуокружностями и общей базовой линией (рис. 2). Архимед, вероятно, был первым, кто начал изучать математические свойства арбелоса. Эти свойства описаны в теоремах с 4-ой по 8-ую его книги
Liber assumptorum (или
Книги лемм). Возможно, эту работу написал не Архимед. Сомнения появились после перевода с арабского
Книги лемм, в которой Архимед упоминается неоднократно, но ничего не сказано о его авторстве (однако, существует мнение, что эта книга — подделка [4]).
Книга Лемм так же содержит знаменитую архимедову
Problema Bovinum [5].
Эта статья направлена на систематическое изложение некоторых свойств арбелоса и не носит исчерпывающий характер. Наша цель состоит в том, чтобы выработать единую вычислительную методологию для того, чтобы преподнести данные свойства в формате обучающей статьи. Все свойства выстроены в рамках определённой последовательности и представлены с доказательствами. Эти доказательства были реализованы посредством тестирования эквивалентных вычисляемых утверждений. В ходе выполнения данной работы автором было совершено несколько открытий и сделано несколько обобщений.


 Сидел я как-то дома, читал
Сидел я как-то дома, читал 







 «Программирование без эго» — перевод понятия
«Программирование без эго» — перевод понятия  Привет, Хабр, давно не виделись. В этом посте мне хотелось бы рассказать о таком относительно новом понятии в машинном обучении, как
Привет, Хабр, давно не виделись. В этом посте мне хотелось бы рассказать о таком относительно новом понятии в машинном обучении, как