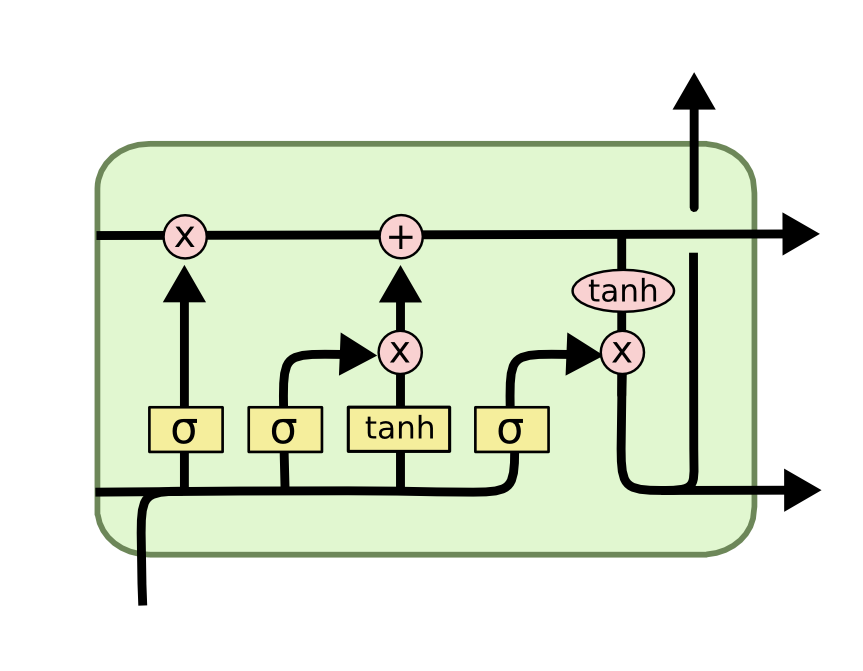
В этой статье я расскажу о том, как работает жидкокристаллический индикатор (ЖКИ) с точки зрения сигналов, как эти сигналы декодировать и использовать для своих целей.

RFID-метка для пациентов, чтобы их было видно на карте больницы

— А можете каждому строителю чип в голову вшить?
— Теоретически да, но, может быть, объясните, зачем вам это нужно?
— Они у нас стройматериалы воруют. Прямо во время работ. А так каждого будет видно, куда он там зашёл, куда не надо.

Проект решился вшиванием в форменную одежду RFID-метки, разделением стройки на зоны и дальше тем, что делается в сети при построении периметра. То есть построением профиля «белого» трафика — кто, куда и когда ходит. А потом — как на файрволле — запретили строителям всё остальное. Кражи сразу сократились. Прораб получил потустороннюю силу и видел почти каждый косяк.

А дальше каждый чёртов раз, когда я рассказываю про RFID-решение, люди начинают махать руками и путать эти метки с Wi-Fi, Bluetooth и пассивными резонирующими контурами. Одна из причин — некоторые RFID-метки действительно работают по Wi-Fi 802.11. Давайте расскажу, как это используется на практике в разных странах.

Вышел третий выпуск подкаста Habr Weekly. Обсуждаем победу Рунета над телевидением, новые процессоры от ARM, новость о создании в России единой системы управления госданными, опыт жизни без смартфона в 2019 году и советские мечты о будущем.

Автор: cuamckuu

Извлечение содержимого карты и работа с EMV-командами может быть интересна не только в исследовательских целях. Существует несколько видов атак на бесконтактные банковские карты, про реализацию которых будет рассказано под катом.

Автоматическое сочинение музыки

Почти сразу после того, как я научился программированию, мне хотелось создать ПО, способное сочинять музыку.

Я в течение нескольких лет предпринимал примитивные попытки автоматического сочинения музыки для Visions of Chaos. В основном при этом использовались простые математические формулы или генетические мутации случайных последовательностей нот. Добившись недавно скромного успеха в изучении и применении TensorFlow и нейронных сетей для поиска клеточных автоматов, я решил попробовать использовать нейронные сети для создания музыки.

Как это работает

Композитор обучает нейросеть с долгой кратковременной памятью (Long short-term memory, LSTM). LSTM-сети хорошо подходят для предсказания того, «что встретится дальше» в последовательностях данных. Подробнее о LSTM можно прочитать здесь.


LSTM-сеть получает различные последовательности нот (в данном случае это одноканальные файлы midi). После достаточного обучения она получает возможность создавать музыку, схожую с обучающими материалами.

Распространение приложений вроде Waze, Apple Maps и Google Maps умножает хаос

Мигель-стрит – это извилистая узкая дорога, проходящая по району Глен-Парк города Сан-Франциско. Ещё несколько лет назад по ней ездили только жители окрестных домов, и они хорошо знали все её проблемы. Теперь она забита машинами, которые используют её как короткий путь от переполненной Мишн-стрит до популярной Маркет-стрит. Местные жители с трудом добираются до дома, а ДТП случаются ежедневно.

Эта проблема началась, когда приложения Waze, Apple Maps и Google Maps получили широкое распространение, и начали предлагать водителям объезды пробок в реальном времени. Во всём мире такими приложениями пользуется порядка миллиарда водителей.

Сегодня транспортные пробки появляются неожиданно, в местах, ранее бывших спокойными, во всех городах и странах мира. В Бостоне, в районе Дорчестер жители Адамс-стрит жалуются на быстро движущиеся в час пик машины, водители многих из которых уставились вниз, на свои телефоны, планируя следующий манёвр. Лондонские объездные пути, ранее бывшие секретным достоянием таксистов, теперь заполнены пользователями приложений. Одним из первых от этой напасти пострадал Израиль, поскольку именно там основали Waze; там быстро развился такой хаос, что один из жителей Герцлия-бет даже засудил компанию.

Однажды мой знакомый, который на тот момент администрировал некое веб-приложение на сервере под управлением GNU/Linux, пожаловался на одного вредного администратора сервера. Тот ни в какую не хотел устанавливать htop, несмотря на все просьбы.

Я немного удивился и поинтересовался, в чём причина такого странного поведения. Если упростить, то дальнейший наш диалог получился вот таким:

Несколько лет назад, когда был выпущен первый релиз Cogmind, я без предрассудков относился к выпуску официальной версии под Mac. В конце концов, Cogmind — моя первая коммерческая игра, раньше я выпускал только хобби-проекты в статусе freeware и только под Windows, поэтому не был уверен, какие результаты даст поддержка дополнительных платформ. Поэтому я решил подождать и посмотреть стоит ли в каком-то виде реализовывать официальную поддержку на Mac.

Тем временем я убедился, что Cogmind (и другое моё ПО) идеально работает через Wine и подобные ему пакеты. Разумеется, в Steam я никогда не говорил о поддержке Mac, потому что это не был отдельный скачиваемый файл, работающий сам по себе. Я готовился к выпуску версии 1.0, и откладывал решение о том, стоит ли принимать меры для реализации полной поддержки платформы, на будущее.

На текущий момент я уже достаточно прождал и увидел, чтобы прийти к осмысленному решению: официальная поддержка macOS просто недостижима для меня.

Почему такое решение было принято именно сейчас: если вы следите за разработчиками инди-игр, сообществами или новостями, то должны были слышать о шумихе, связанной с Apple. К сожалению, мой голос тоже присоединится к этому хору.

В последнем подкасте Habr Weekly #21 обсуждалась тема отслеживающих cookies и вопрос их нежелательности. Бытуют мнения о сомнительности вреда таких куков если скрывать и вправду нечего. Такая позиция определенно не выдерживает критики.

На прошлой неделе получила развитие история про атаки на уязвимый софт в SIM-картах. Обнаруженная ранее активно эксплуатируемая атака SimJacker оказалась не единственной. Исследователи из компании Ginno Security сообщили о похожей проблеме в компоненте Wireless Internet Browser (новость, пост в блоге компании). Хотя уязвимость в WIB сложнее в эксплуатации, чем проблема в S@T Browser, метод похож: присылаем подготовленную SMS, которая без ведома владельца позволяет совершить звонок, отправить сообщение или получить IMEI телефона.

Первый репорт об уязвимости в S@T Browser вообще выглядел довольно странно: о проблеме сообщает единственная компания, потенциальный ущерб оценить сложно, а оценка количества подверженных устройств выглядит преувеличенной: сотни миллионов. Поэтому в исследовании Ginno Security важна даже не сама уязвимость, а подтверждение актуальности проблемы из второго источника. Впрочем, еще один эксперт по безопасности мобильной связи, Карстен Нол, считает, что атаки такого плана слишком сложны для массовой эксплуатации: проще клонировать SIM-карту методами социальной инженерии или воспользоваться уязвимостями протокола SS7, по которому взаимодействуют между собой операторы.

Всем привет! Мы продолжаем работать над игрой “мечты” Another Way. Это уже третий пост на эту тему, с предыдущим вы можете ознакомиться по ссылке — Через тернии к игре мечты — месяц спустя. Я не писал о прогрессе чуть более месяца, скопилось много много информации, поэтому будет минимум текста, но много картинок. Всем тем кто не боится трафика — добро пожаловать под кат.

Введение

На данный момент, на рынке представлен большой ассортимент одноплатников на любой вкус по приемлемой цене.

Как правило, различные сборки от производителей, предназначены для оценки платформы и являются отправной точкой нового проекта, поэтому не всегда подходят под конкретные задачи. В задачах где требуется высокая надежность, перед разработчиком встает вопрос, как доработать дистрибутив и потом не поплатиться за это полной переработкой образа и системы обновления.

За последний год я сталкивалась с необходимостью рисования гистограмм и столбчатых диаграмм достаточно часто для того, чтобы появилось желание и возможность об этом написать. Кроме того, мне самой довольно сильно не хватало подобной информации. В этой статье приведен обзор 3 методов создания таких графиков на языке Python.

Начнем с того, чего я сама по своей неопытности не знала очень долго: столбчатые диаграммы и гистограммы — разные вещи. Основное отличие состоит в том, что гистограмма показывает частотное распределение — мы задаем набор значений оси Ox, а по Oy всегда откладывается частота. В столбчатой диаграмме (которую в англоязычной литературе уместно было бы назвать barplot) мы задаем и значения оси абсцисс, и значения оси ординат.

Для демонстрации я буду использовать избитый набор данных библиотеки scikit learn Iris. Начнем c импортов:

import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()

Преобразуем набор данных iris в dataframe — так нам удобнее будет с ним работать в будущем.

data = pd.DataFrame(data= np.c_[iris['data'], iris['target']], columns= iris['feature_names'] + ['target'])

Из интересующих нас параметров data содержит информацию о длине чашелистиков и лепестков и ширине чашелистиков и лепестков.

Используем Matplotlib
Построение гистограммы
Cтроим обычную гистограмму, показывающую частотное распределение длин лепестков и чашелистиков:

fig, axs = plt.subplots(1, 2)
n_bins = len(data)
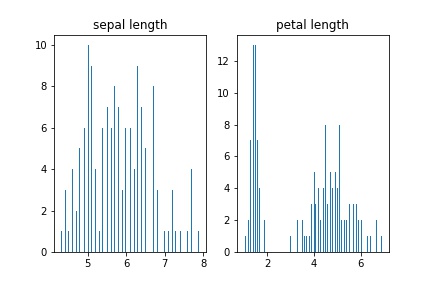
axs[0].hist(data['sepal length (cm)'], bins=n_bins)
axs[0].set_title('sepal length')
axs[1].hist(data['petal length (cm)'], bins=n_bins)
axs[1].set_title('petal length')

В статье подробно, вплоть до самых мелочей, рассмотрены три способа взятия интеграла Эйлера-Пуассона. В одном из способов выводится вспомогательная формула редукции. Для нахождения некоторых сложных интегралов можно использовать формулы редукции, которые позволяют понизить степень подынтегрального выражения и вычислить соответствующие интегралы за конечное число шагов.

Это вторая и последняя часть моей шпаргалки по аббревиатурам, которые стоит знать C++ разработчику. С++ здесь упомянут только потому, что шпаргалку я составил в первую очередь для себя, а я как раз-таки C++ разработчик.

На самом деле в этой части собраны понятия, область применения которых не ограничена C++. Так что подборка может быть интересна более широкой аудитории.

Меня зовут Вячеслав, я хронический математик и уже несколько лет не использую циклы при работе с массивами…

Ровно с тех пор, как открыл для себя векторные операции в NumPy. Я хочу познакомить вас с функциями NumPy, которые чаще всего использую для обработки массивов данных и изображений. В конце статьи я покажу, как можно использовать инструментарий NumPy, чтобы выполнить свертку изображений без итераций (= очень быстро).

Не забываем про

import numpy as np

и поехали!

Введение

fBM расшифровывается как Fractional Brownian Motion (дробное броуновское движение). Но прежде чем начать говорить о природе, фракталах и процедурных рельефах, давайте на минуту углубимся в теорию.

Броуновское движение (Brownian Motion, BM), просто, без «дробности» — это движение, при котором положение объекта с течением времени меняется со случайными инкрементами (представьте последовательность position+=white_noise();). С формальной точки зрения BM является интегралом белого шума. Эти движения задают пути, которые являются случайными, но (статистически) самоподобными, т.е. приближенное изображение пути напоминает весь путь. Fractional Brownian Motion — это схожий процесс, в котором инкременты не полностью независимы друг от друга, а в этом процессе существует некая память. Если память имеет положительную корреляцию, то изменения в заданном направлении будут иметь тенденцию к будущим изменениям в том же направлении, и путь при этом будет плавнее, чем при обычном BM. Если память имеет отрицательную корреляцию, то за изменением в положительную сторону с большой вероятностью последует изменение в отрицательную, и путь окажется гораздо более случайным. Параметр, управляющий поведением памяти или интегрированием, а значит и самоподобием, её размерностью фрактала и спектром мощности, называется показателем Хёрста и обычно сокращается до H. С математической точки зрения H позволяет нам интегрировать белый шум только частично (допустим, выполнить только 1/3 интегрирования, отсюда и «дробность» в названии) для создания fBM под любые нужные нам характеристики памяти и внешний вид. H принимает значения в интервале от 0 до 1, которые описывают, соответственно, грубое и плавное fBM, а обычное BM получается при H=1/2.


Здесь функция fBM() использована для генерации рельефа, облаков, распределения деревьев, вариаций их цветов и деталей крон. «Rainforest», 2016: https://www.shadertoy.com/view/4ttSWf

На WWDC 2019 Apple в очередной раз нарушила покой iOS разработчиков — представила новую систему авторизации пользователей Sign in with Apple. Теперь все iOS приложения, которые используют сторонние системы авторизации (Facebook, Twitter, etc.), должны в обязательном порядке реализовать Sign in with Apple, иначе выгонят из AppStore. Мы решили не испытывать судьбу и побежали внедрять эту фичу. Как именно мы это сделали — узнаете под катом.

Сколько еще будет найдено применений дронов? Все привыкли, что квадрокоптер должен быть обязательно с камерой и что-нибудь снимать, но разработчики из Intel показали нам новые области применения. Речь идет о световых шоу, построенных с помощью большого количества дронов, когда каждый дрон — это светящаяся точка и вместе эти точки образуют трехмерные фигуры в ночном небе. Компании, предоставляющие такие услуги, появляются с удивительной скоростью. Спроса на рынке больше, чем предложения. Так что же нужно, чтобы запустить в воздух сотни дронов? Задача нетривиальная и очень интересная, поэтому, как участник зарождающегося направления, хочу поделиться впечатлениями от того, что есть на текущий момент и раскрыть тонкости этой индустрии.

При первом знакомстве с квазиньютоновскими методами можно удивиться дважды. Во-первых, после беглого взгляда на формулы охватывают сомнения, что это вообще может работать. Однако же они работают. Дальше кажется сомнительным, что они будут работать хорошо. И тем удивительнее видеть то, насколько они превосходят по скорости разнообразные вариации градиентного спуска, причем не на специально построенных задачах, а на самых настоящих, взятых из практики. И если после этого еще остаются сомнения вперемешку с интересом — то нужно разбираться в том, почему вообще работает это нечто.