User
Интерактивная карта клиентов — Apache Spark Streaming и Яндекс.Карты
- изменение котировок
- действия пользователей в онлайн-игре
- отображала агрегированную информацию из соцсетей в различных проекциях
и т.д. Если вы так не умеете, то смузи уже не нальют.

Магия тензорной алгебры: Часть 8 — О свертках тензора Леви-Чивиты
Содержание
- Что такое тензор и для чего он нужен?
- Векторные и тензорные операции. Ранги тензоров
- Криволинейные координаты
- Динамика точки в тензорном изложении
- Действия над тензорами и некоторые другие теоретические вопросы
- Кинематика свободного твердого тела. Природа угловой скорости
- Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
- О свертках тензора Леви-Чивиты
- Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
- Получаем вектор угловой скорости. Работаем над недочетами
- Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
- Параметры Родрига-Гамильтона в кинематике твердого тела
- СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
- Нестандартное введение в динамику твердого тела
- Движение несвободного твердого тела
- Свойства тензора инерции твердого тела
- Зарисовка о гайке Джанибекова
- Математическое моделирование эффекта Джанибекова
Введение
В прошлой статье мы напоролись на конструкцию вида
Итак, поговорим о свертках тензора Леви-Чивиты.
Магия тензорной алгебры: Часть 4 — Динамика точки в тензорном изложении
Содержание
- Что такое тензор и для чего он нужен?
- Векторные и тензорные операции. Ранги тензоров
- Криволинейные координаты
- Динамика точки в тензорном изложении
- Действия над тензорами и некоторые другие теоретические вопросы
- Кинематика свободного твердого тела. Природа угловой скорости
- Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
- О свертках тензора Леви-Чивиты
- Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
- Получаем вектор угловой скорости. Работаем над недочетами
- Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
- Параметры Родрига-Гамильтона в кинематике твердого тела
- СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
- Нестандартное введение в динамику твердого тела
- Движение несвободного твердого тела
- Свойства тензора инерции твердого тела
- Зарисовка о гайке Джанибекова
- Математическое моделирование эффекта Джанибекова
Введение
Итак, настал момент применить на практике всё то, о чем мы так долго рассуждали теоретически. Данная заметка будет использовать в основном материал предыдущей статьи, в которой есть ссылки на предыдущие публикации по тензорной тематике.
А заниматься мы будем механикой. Именно решение задач механики и побудило меня разбираться с тензорным исчислением. И поговорим мы об уравнениях Лагранжа 2 рода, которые применяются для анализа движения сложных механических систем. Эти уравнения имеют вид, хорошо известный большинству специалистов в данной области
где s — число степеней свободы механической системы;
Те, кто сталкивался с этими уравнениями наверняка замечали, что после выполнения трехкратного дифференцирования кинетической энергии получаются выражения, представленные линейной комбинацией вторых производных от обобщенных координат и линейной комбинации произведений их первых производных. И это, по крайней мере меня, наводило на мысль о том, что кинетическую энергию можно продифференцировать один раз в общем виде, а потом просто составлять уравнения движения, используя полученные выражения общего вида. Только вот попытки проделать это самостоятельно не приводили меня к успеху.
Тем не менее это можно сделать, если опираться на тензорное исчисление, в общем и не прибегая к дифференцированию кинетической энергии (хотя такой подход тоже возможен). И мы сделаем это в данной статье, правда пока только для точки, и заодно решим какую-нибудь не слишком сложную задачку, иллюстрирующую эффективность рассмотренного подхода.
Что же, начнем!
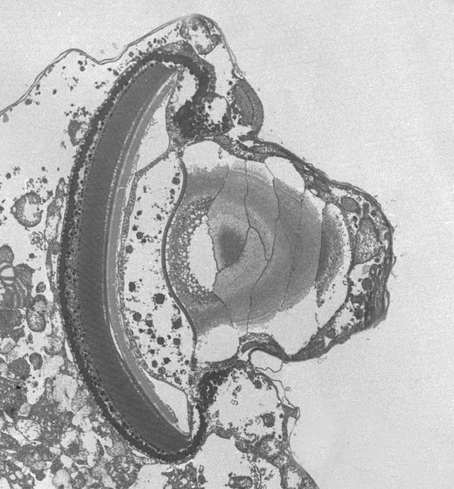
У одноклеточных нашли копию глаза высших животных: подобие глаза состоит из элементов, напоминающих хрусталик, роговицу, зрачок и сетчатку
Магия тензорной алгебры: Часть 3 — Криволинейные координаты
Содержание
- Что такое тензор и для чего он нужен?
- Векторные и тензорные операции. Ранги тензоров
- Криволинейные координаты
- Динамика точки в тензорном изложении
- Действия над тензорами и некоторые другие теоретические вопросы
- Кинематика свободного твердого тела. Природа угловой скорости
- Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
- О свертках тензора Леви-Чивиты
- Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
- Получаем вектор угловой скорости. Работаем над недочетами
- Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
- Параметры Родрига-Гамильтона в кинематике твердого тела
- СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
- Нестандартное введение в динамику твердого тела
- Движение несвободного твердого тела
- Свойства тензора инерции твердого тела
- Зарисовка о гайке Джанибекова
- Математическое моделирование эффекта Джанибекова
Введение
Читая отзывы к своим статьям, понял, что я излишне перегрузил читателя теоретическими вводными. Прошу за это прощения, признаться честно, я сам далек от формальной математики.
Однако, тензорное исчисление пестрит понятиями, многие из которых требуется вводить формально. Поэтому третья статься цикла тоже будет посвящена сухой теории. Тем не менее, я обещаю, что в следующей работе приступлю к тому, к чему сам давно хотел — к описанию практической ценности тензорного подхода. На примете имеется интересная задача, большая часть которой в моей голове уже разобрана. Тензорное исчисление для меня не праздный интерес, а способ обработать некоторые из своих теоретических и практических соображений в области механики. Так что практика по полной программе ещё предстоит.
А пока что рассмотрим некоторые теоретические основы. Добро пожаловать под кат.
Как технологии украли время на креативность

Оригинал: How Technology Has Hijacked Our Creative Spaces
Нам в буквальном смысле надо давать себе отдых от технологий, чтобы освободить разум.
Недавно я поняла, что креативные идеи посещают меня в то время, когда… Интернет отключен, а Wi-Fi не доступен. Или когда я иду выгуливать собаку и забываю смартфон. Или когда я еду домой, а батарея смартфона разряжена.
Да, конечно. Я прекрасно понимаю, что это далеко не новость. Или, может кто-то об этом еще не знает? Что касается меня, то это умозаключение открыло глаза на многое. Я никогда не хотела считать, что современные технологии — что-то, что может мешать мне быть креативной. Наоборот, я всегда думала, что технологии помогают креативности. Я могу читать интересные статьи, где и когда хочу. Я могу продуктивно использовать каждую минуту свободного времени. Всего пару нажатий на экран смартфона, и я могу получить доступ к нескончаемым запасам информации и знаний.
Но что толку? Какой смысл напичкивать себя информацией, если времени ее переработать и усвоить все равно нет?
Шведские учёные создали искусственный нейрон, способный общаться с живыми нейронами
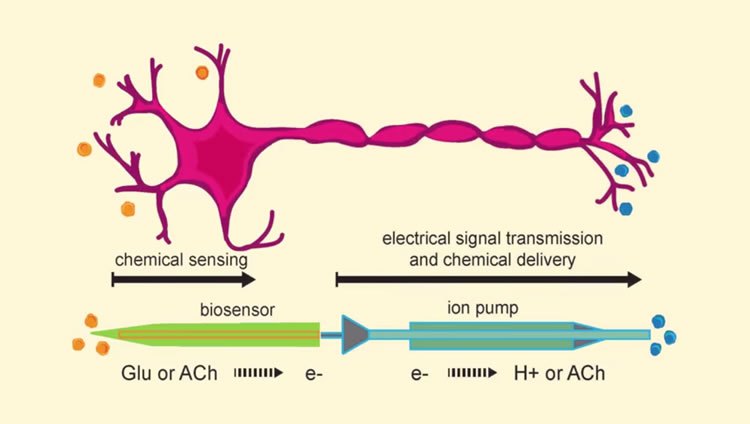
Шведские учёные из Каролинского института сумели создать полностью рабочий искусственный нейрон на основе органической биоэлектроники. В нём нет «живых» частей, но он способен имитировать работу нервных клеток мозга и общаться с другими нейронами.
Нейрон — специализированная клетка центральной нервной системы. Они образуют нейронные сети, в которых клетки общаются друг с другом посредством сигналов. Сигналы испускаются и распространяются клетками с помощью ионов, генерирующих электрический заряд, который движется по телу нейрона. Заряд идёт по аксону (длинному отростку), доходит до окончания, где в синапсе преобразовывается в химические передатчики сигналов — нейромедиаторы (или нейротрансмиттеры).
Нейромедиаторы — это биологически активные химические вещества, которые передают импульсы от нервной клетки через синаптическое пространство между нейронами, а также, например, от нейронов к мышечной ткани.
Неизвестная история Tesla, часть 3/3
Итак, в результате массивной пиар-кампании Tesla Motors получила известность и заказы, а Эберхард стал самой настоящей звездой. К примеру, в 2006 году его лицо появилось в рекламе BlackBerry Pearl. Если верить Research in Motion, его заслуга была в том, что он создал первый спортивный электромобиль. Между тем Илону Маску распределение ролей приходилось не по душе. В электронном письме Харригану от 18 июля 2006 года он пишет:
«Ситуация с тем, как на данный момент изображают мою роль, и что меня называют всего лишь «ранним инвестором», является вопиющей. Это всё равно, что назвать Мартина [Эберхарда] «ранним сотрудником».
В дополнение к ведущей роли в первом и втором раунде инвестирования и участии в третьем моё влияние на собственно автомобиль распространяется от фар до порога дверей и багажника. Мой сильный интерес к электрическому транспорту превосходит возраст Tesla на десятилетие. Конечно, Мартин должен быть центральной фигурой, но на данный момент изображение моей роли было чрезвычайно оскорбительно.
Я не обвиняю тебя или других сотрудников Tesla — СМИ управлять сложно. Однако, нам нужно проявить серьёзные усилия для коррекции этого восприятия.»
Неизвестная история Tesla, часть 2/3
Создание первого электромобиля

Основные положения оригинального бизнес-плана Tesla
Ближе к осени 2003 года Эберхард и Тарпеннинг решили продумать основные идеи компании перед тем, как искать инвесторов, чтобы так резко не напугать их своей странноватой идеей. Было решено работать с уже известными инвесторами, которые никогда бы не стали вкладываться в электрокары. Их интересовали лишь технологии передачи данных по оптоволокну и дизайн веб-сайтов. Это были компании, с которыми основатели Tesla уже были знакомы по трём раундам инвестирования в NuvoMedia, их первой успешной компании по производству устройств чтения электронных книг.
Свой облачный хостинг за 5 минут. Часть 1: Ansible, Docker, Docker Swarm

Привет Хабр! Последние 1.5 года я работал над своим проектом, которому был необходим надежный облачный хостинг. До этого момента я больше 10 лет занимался веб-программированием и когда я решил построить свой хостинг у меня были относительно поверхностные знания в этой области, я и сейчас не являюсь системным администратором. Все что я буду рассказывать может выполнить обычный программист в течение 5 минут, просто запустив набор сценариев для Ansible, которые я подготовил специально для вас и выложил на GitHub.
Лекция Дмитрия Ветрова о математике больших данных: тензоры, нейросети, байесовский вывод
Как можно хранить и обрабатывать многомерные массивы в линейных по памяти структурах? Что дает обучение нейронных сетей из триллионов триллионов нейронов и как можно осуществить его без переобучения? Можно ли обрабатывать информацию «на лету», не сохраняя поступающие последовательно данные? Как оптимизировать функцию за время меньшее чем уходит на ее вычисление в одной точке? Что дает обучение по слаборазмеченным данным? И почему для решения всех перечисленных выше задач надо хорошо знать математику? И другое дальше.
Люди и их устройства стали генерировать такое количество данных, что за их ростом не успевают даже вычислительные мощности крупных компаний. И хотя без таких ресурсов работа с данными невозможна, полезными их делают люди. Сейчас мы находимся на этапе, когда информации так много, что традиционные математические методы и модели становятся неприменимы. Из лекции Дмитрия Петровича вы узнаете, почему вам надо хорошо знать математику для работы с машинным обучением и обработкой данных. И какая «новая математика» понадобится вам для этого. Слайды презентации — под катом.
Краткое введение в тензоры
Сейчас я попытаюсь дать совсем простое введение в тензоры. Я не претендую на математическую строгость, поэтому некоторые термины могут употребляться не совсем корректно.
Магия тензорной алгебры: Часть 2 — Векторные и тензорные операции. Ранги тензоров
Содержание
- Что такое тензор и для чего он нужен?
- Векторные и тензорные операции. Ранги тензоров
- Криволинейные координаты
- Динамика точки в тензорном изложении
- Действия над тензорами и некоторые другие теоретические вопросы
- Кинематика свободного твердого тела. Природа угловой скорости
- Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
- О свертках тензора Леви-Чивиты
- Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
- Получаем вектор угловой скорости. Работаем над недочетами
- Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
- Параметры Родрига-Гамильтона в кинематике твердого тела
- СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
- Нестандартное введение в динамику твердого тела
- Движение несвободного твердого тела
- Свойства тензора инерции твердого тела
- Зарисовка о гайке Джанибекова
- Математическое моделирование эффекта Джанибекова
Введение
Несказанно рад, что читателям понравилась предыдущая статья. Сразу сделаю оговорку — просто рассказать о таком ёмком понятии как тензор не получится — велик объем информации. Могу обещать, что к концу цикла мозаика сложится.
А в прошлый раз мы остановились на том, что рассмотрев представление вектора в косоугольном базисе, и определив, что он представляется двумя разными (ковариантными и контравариантными) наборами координат, получили общие выражения для скалярного произведения, учитывающие изменение метрики пространства. Таким образом, мы весьма осторожно подошли к понятию тензора
Тензор — математический объект, не изменяющийся при изменении системы координат, представленный набором >своих компонент и правилом преобразования компонент при смене базиса.
Скалярное произведение — это хорошо. Но как же быть с остальными операциями? Как они связываются с геометрией пространства и представимы ли в тензорном виде? Разумеется представимы, ведь векторы — это… тензоры! И скаляры — это тоже тензоры. Привычные нам математические объекты лишь частные примеры более общего понятия, коим является тензор.
Вот об этом мы и поговорим под катом.
Магия тензорной алгебры: Часть 1 — что такое тензор и для чего он нужен?
Содержание
- Что такое тензор и для чего он нужен?
- Векторные и тензорные операции. Ранги тензоров
- Криволинейные координаты
- Динамика точки в тензорном изложении
- Действия над тензорами и некоторые другие теоретические вопросы
- Кинематика свободного твердого тела. Природа угловой скорости
- Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
- О свертках тензора Леви-Чивиты
- Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
- Получаем вектор угловой скорости. Работаем над недочетами
- Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
- Параметры Родрига-Гамильтона в кинематике твердого тела
- СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
- Нестандартное введение в динамику твердого тела
- Движение несвободного твердого тела
- Свойства тензора инерции твердого тела
- Зарисовка о гайке Джанибекова
- Математическое моделирование эффекта Джанибекова
Введение
Это было очень давно, когда я учился классе в десятом. Среди довольно скудного в научном плане фонда районной библиотеки мне попалась книга — Угаров В. А. «Специальная теория относительности». Эта тема интересовала меня в то время, но информации школьных учебников и справочников было явно недостаточно.
Однако, книгу эту я читать не смог, по той причине, что большинство уравнений представлялись там в виде тензорных соотношений. Позже, в университете, программа подготовки по моей специальности не предусматривала изучение тензорного исчисления, хотя малопонятный термин «тензор» всплывал довольно часто в некоторых специальных курсах. Например, было жутко непонятно, почему матрица, содержащая моменты инерции твердого тела гордо именуется тензором инерции.
Тестирование светодиодных ламп IKEA
Одни из самых низких цен на светодиодные лампы сейчас в магазинах IKEA.
Я протестировал 11 актуальных светодиодных ламп LEDARE, стоящих от 169 до 599 рублей.

Анализ SSL/TLS трафика в Wireshark

Как скрыть от посторонних конфиденциальную информацию?
Самое простое – зашифровать.
В Интернет и Интранет-сетях шифрацией данных управляет протокол SSL/TLS.
Солдат спит, служба идет.
Однако иногда возникает необходимость выполнить обратное – расшифровать перехваченный трафик.
Это может потребоваться как для отладки работы приложений, так и для проверки подозрительной сетевой активности.
Или в целях изучения работы SSL/TLS (очевидные, вредоносные цели не обсуждаются).
Как и при каких условиях можно расшифровать дамп SSL/TLS трафика в Wireshark?
Попробуем разобраться.
Детский лагерь: биссектрально-пифагоровы треугольники, перепрограммирование мозга, радар-детектор и взлом наручников

Часть вещей, которые я взял с собой на смену
Я думал, что я самый безбашенный человек в лагере, пока не приехал преподаватель Яндекса. Босиком. Он отпил глоток воды из графина и сказал: «Эээх, раньше я так водку пил». Затем он прочитал искрометную лекцию и «нарисовал» множество эллиптических кривых.
Вот как Алексей Савватеев анонсировал свою лекцию:
В журнале «Квант» номер 8 за 1983 год в статье «Вокруг биссектрисы» на странице 36 И.Ф.Шарыгин формулирует такую задачу:
«Про данный треугольник известно, что треугольник, образованный основаниями его биссектрис — равнобедренный. Можно ли утверждать, что и данный треугольник равнобедренный?»
Ответ отрицательный, но в статье далее сказано:
«К сожалению, автор не сумел построить конкретный пример треугольника (то есть точно указать величины всех его углов или длины сторон) со столь экзотическим свойством. Может быть, это удастся сделать читателям журнала?»
С тех пор построены три примера. Последний пример выводит нас на теорию эллиптических кривых и операцию сложения точек.
В лекции мы построим ЦЕЛОЧИСЛЕННЫЙ треугольник, обладающий требуемым свойством. Вопрос о бесконечности таких треугольников пока ещё остаётся открытым. Школьная задача, таким образом, приведёт нас в самое сердце одной из красивейших ветвей современной математики.
Смена в самом разгаре, кое-что интересное мы уже успели сделать, а что-то еще в планах.
«pip -t» — простая альтернатива virtualenv
TL;DR
Чтобы просто установить и изолировать зависимости проекта, virtualenv часто оказывается слишком тяжелым решением. Предлагаем простую альтернативу:
- добавить
./.pipв переменную окруженияPYTHONPATH, - установить пакеты локально с помощью
pip install -t .pip, - запускать
pythonиз папки проекта.
Information
- Rating
- Does not participate
- Registered
- Activity