Инженер-программист
Установка расширения в браузер возможна благодаря такой замечательной штуке, как manifest.json. Но что он может скрывать и почему важно изучать (по возможности) манифест перед установкой. Сегодня мы это разберем!
В последние месяцы в киберпространстве развернулась настоящая война, отчего незащищенные информационные активы значительно пострадали, а пользователи защитного инструментария от западных «партнеров» столкнулись с серьезнейшими санкциями, ограничивающими использование их ПО. Поэтому мы решили посмотреть на рынок отечественного ПО, разработанного для усиления «инфобеза».
Обычно на вопрос "Какой сканер безопасности купить?" вспоминаются лишь OpenVas и Nessus (Tenable). Но есть и другие достойные отечественные продукты, о которых мы сегодня и поговорим – это продукты для корпоративного сегмента, полностью лицензированные под все российские требования безопасности и имеющие сертификаты ФСТЭК и ФСБ:
Конец 18-го и 19-й век были временем колоссального прогресса в математике. Величайшие умы тысячелетия вводили все новые математические системы и языки, такие как алгебры Клиффорда и Грассмана. Хотя эти алгебры вызвали значительный интерес, в то время они воспринимались как подспорье более прямолинейной и более общеприменимой векторной алгебры Гиббса. Это было фактически концом поисков объединяющего математического языка и началом распространения новых алгебраических систем, создаваемых по мере необходимости; например, спинорная алгебра, матричная и тензорная алгебры, дифференциальные формы и т. д.
В этой статье мы реализуем возрождение алгебр Клифорда и Грассмана в виде структуры, известной как геометрическая алгебра (ГА). Это понятие было впервые введено в середине 1960-х годов американским физиком и математиком Дэвидом Хестенсом. Прошло 40 лет, но есть признаки того, что его утверждение о том, что ГА является универсальным языком для физики и математики, теперь начинает принимать все более явственные очертания. Во всем мире растет число групп, которые применяют ГА к целому ряду проблем из многих научных областей, обеспечивая чрезвычайно мощную математическую структуру, в которой могут быть выражены самые передовые концепции квантовой механики, теории относительности, электромагнетизма и т. д. При этом, утверждается, что ГА также достаточно проста для преподавания школьникам! В этой статье мы рассмотрим развитие и недавний прогресс ГА и обсудим, действительно ли она является объединяющим языком для физики и математики 21-го века. Примеры, которые мы будем использовать для иллюстрации, будут взяты из ряда областей физики и техники.
Написано довольно много хороших материалов о свободных лицензиях, в том числе тут, на Habr. Почему стоит прочитать еще и эту статью:
На прошлой неделе компания Monotype — владелец прав на популярные шрифты Times New Roman, Verdana, Arial, Helvetica и Tahoma — объявила об ограничении доступа из России к своей библиотеке и сообщила о приостановке взаимодействия с российскими организациями. Новость стала еще одним поводом обратить внимание на специфику использования проприетарных шрифтов в бизнес-среде – проблему, которая выходит далеко за рамки ситуации с Monotype. Речь о возможных сложностях при отображении существующих документов и шаблонов, особенно при работе с различными таблицами, формами и автоматически формируемыми файлами из информационных систем.
Для минимизации подобных проблем мы в МойОфис еще шесть лет назад представили свои шрифты XO_Fonts. Они свободно распространяются и доступны бесплатно. Сегодня этот набор состоит из 11 шрифтов и 24 начертаний. Их особенностью является метрическая совместимость с распространенными проприетарными шрифтами, которая позволяет сохранить оригинальное форматирование и верстку документов, ранее созданных с использованием популярных иностранных шрифтов.
Некоторое время назад на D-Russia была опубликована история создания XO_Fonts. Теперь мы предлагаем ознакомиться с ней и читателям Хабра.
Некоторое время назад, хаброжитель DmitrySpb79 написал статьи о создании электронных часов. В них он рассмотрел источники точного времени, а так-же элементную базу для создания электронных часов. Были упомянуты Arduino, STM, Raspberry PI, ESP8266, но совсем забыли про ПЛИС. 
"Электроника МС 1504" - первый серийно производившийся советский ноутбук. Внутризаводское обозначение модели - "Электроника ПК 300".
В этой статье мы заглянем в него внутрь, причём в разные его модификации, а также сравним с его прототипом - Тошибой T1100 Plus.
Какое-то время назад я опубликовал статью-презентацию об инструменте под названием QEDA. Если кратко, то это утилита для облегчения процесса создания библиотеки электронных элементов.
Были сделаны полезные выводы, проведена дальнейшая работа, проект развивался. Появился интерфейс коммандной строки (CLI). На сегодняшний день можно говорить о некотором milestone: проект достиг версии 0.1.
В этот статье я рассмотрю типичный рабочий процесс по созданию платы в среде KiCad и использованием утилиты QEDA.
Предупреждение: будут картинки и, как следствие, трафик.
Напишите функцию, выводящую список целых чисел от 1 до 100, но вместо каждого числа, кратного 3, она должна выводить «Fizz», а вместо каждого числа, кратного 5, выводить «Buzz». Вместо чисел, кратных и 3, 5, программа должна выводить «FizzBuzz»; все остальные числа должны выводиться без изменений.
[(lambda n: { 1: n, 6: "Fizz", 10: "Buzz", 0: "FizzBuzz" }[n**4%15])(n+1) for n in range(100)](1..100).map{|n| {1 => n, 6 => "Fizz", 10 => "Buzz", 0 => "FizzBuzz"}[n**4%15] }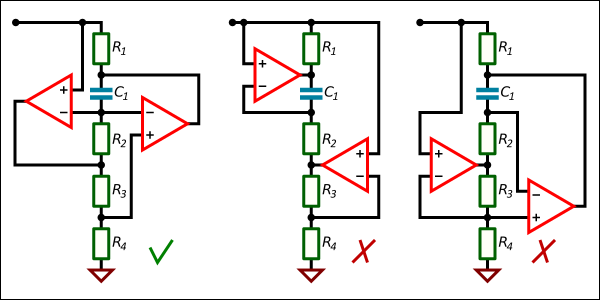
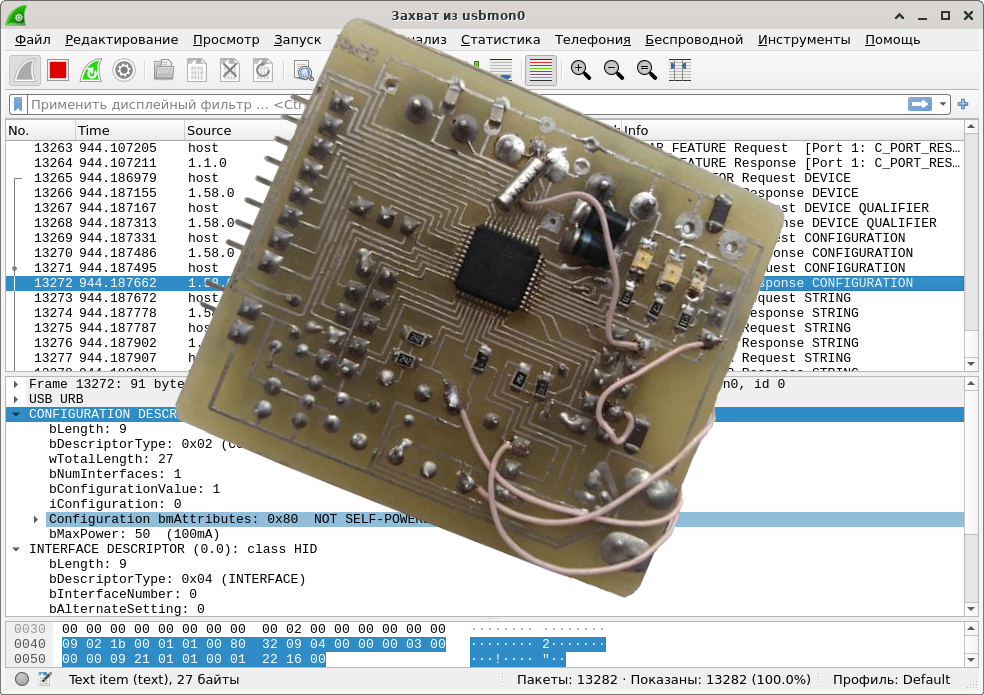
Двадцать лет назад физики начали исследовать загадочную асимметрию внутреннего строения протона. Результаты их работы, опубликованные в конце февраля 2021 года, объясняют, как антивещество помогает стабилизировать ядро каждого атома.
Материал по мотивам методики создания магнитопланарных излучателей для наушников и колонок. Подход имеет широкий спектр применения, не только для создания электроакустических систем. Например, для гибких шлейфов взамен порванных, антенн и прочего, на что хватит воображения и терпения. Один из вариантов использования фоторезистивного метода вместо популярного ЛУТ.
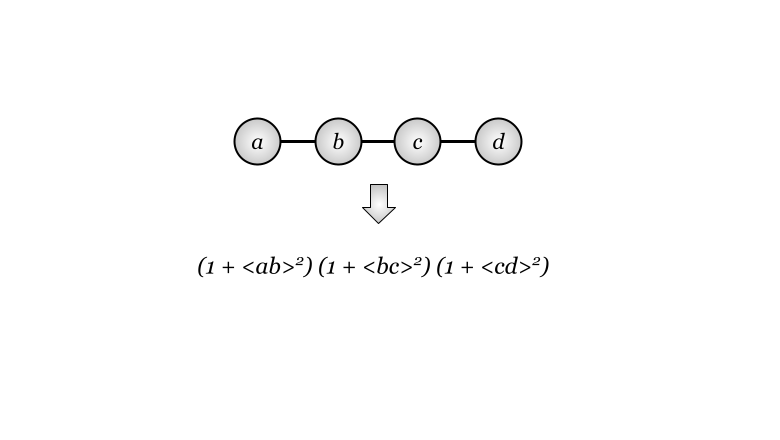
В данной работе мы продолжаем обзор свойств внешней алгебры. В первой части мы определили внешнее произведение элементов, ввели понятие симплексов, границ и копространства. Здесь рассмотрим аффинные пространства, в которых определено скалярное произведение между элементами, их называют также евклидовыми.
Обычно в качестве примера евклидового приводят окружающее нас трехмерное пространство. В нем действительно есть скалярное произведение между элементами и векторами. Но все-таки оно является лишь частным случаем общего семейства евклидовых пространств. Более общим примером являются пространства со связями, в простонародье именуемые графами. Поэтому в основном на метрических свойствах графах мы и сосредоточимся, а в конце покажем, как от графов перейти к обычному пространству.
Я продолжаю изучать CAN шину авто. В предыдущих статьях я голосом открывал окна в машине и собирал виртуальную панель приборов на RPi. Теперь я разрабатываю мобильное приложение VAG Virtual Cockpit, которое должно полностью заменить приборную панель любой модели VW/Audi/Skoda/Seat. Работает оно так: телефон подключается к ELM327 адаптеру по Wi-Fi или Bluetooth и отправляет диагностические запросы в CAN шину, в ответ получает информацию о датчиках.
По ходу разработки мобильного приложения пришлось узнать, что разные электронные блоки управления (двигателя, трансмиссии, приборной панели и др.) подключенные к CAN шине могут использовать разные протоколы для диагностики, а именно UDS и KWP2000 в обертке из VW Transport Protocol 2.0.
В данной статье мы расскажем о том, что такое внешняя алгебра, и для чего она нужна. Удивительно, но на Хабре почти нет статей о внешней алгебре при том, что ее прикладная ценность ничуть не меньше, например, реляционной алгебры.
Наше описание отличается от традиционного изложения в учебниках тем, что мы хотим наполнить внешнюю алгебру прежде всего информатикой, а не геометрией или физикой. Конечная цель статьи - представить произвольный граф в виде алгебраического выражения и показать, что свойства графа можно вычислять как свойства данного выражения. На пути к этому мы познакомимся с основными идеями внешней алгебры.