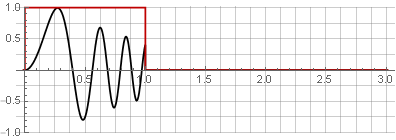
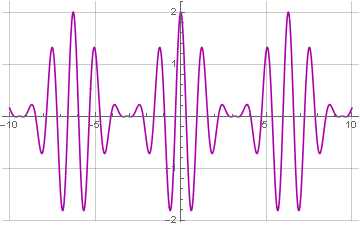
Как посчитать синус быстрее всех на хабре
15 min
Tutorial
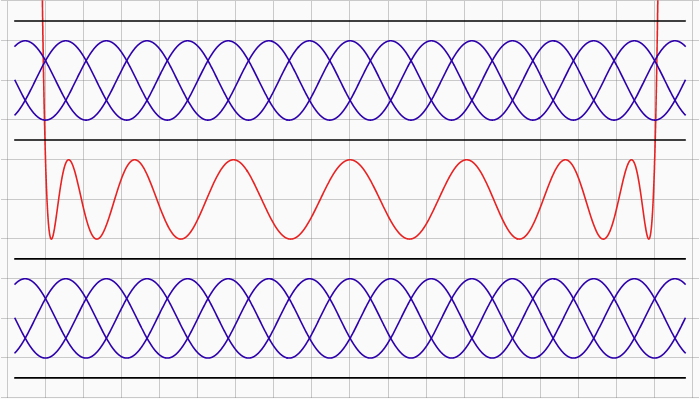
Несмотря на свою кажущуюся банальность, темы о вычислении синуса достаточно регулярно появляются на хабре. И каждый раз их авторы или делают сомнительные утверждения, или получают сомнительные результаты. Не в силах более терпеть, я тоже решил поучаствовать и внести свой, не менее сомнительный вклад в этот вопрос.