Программист
Upd: Поиском по "Upd" можно найти все корректировки, внесенные в статью после публикации в результате жаркой дискуссии в чате Effector.
Меня зовут Андрес, я руководитель команды разработки внутреннего UI-кита ВКонтакте. А это ещё одна статья про инструменты управления состоянием. Сегодня мы не будем изобретать ничего нового, а поговорим про библиотеку Effector.
TL;DR
Почти год мы ВКонтакте пытались внедрить Effector, но пришли к выводу, что пока это достаточно сырая библиотека. Её недостатки зачастую проявляются сильно позже, чем хотелось бы, и, по нашему мнению, перевешивают достоинства… А последние местами преувеличены. Было больно осознавать количество потерянного времени, но, как говорится, лучше поздно, чем никогда.
В сети мало альтернативной информации про Effector, а действительно полезную трудно найти. Надеюсь, эта статья поможет немного исправить ситуацию.
(Внимание, под катом много картинок.)
Привет, Хабр! Меня зовут Влад, я лид направления Web Performance в Тинькофф.
В этом цикле статей я расскажу о подходах, инструментах и показателях, с помощью которых мы наблюдаем за производительностью наших проектов. Но для начала пара слов о том, почему производительность — это важно.
Производительность как один из атрибутов качества программного обеспечения, в значительной степени может влиять на успех конечного продукта. Существует множество историй о том, как даже самые небольшие оптимизации положительно сказывались на опыте взаимодействия и бизнес-показателях компании.
Ведущие игроки IT-индустрии продолжают обращать внимание на важность производительности, проводят масштабные исследования и эксперименты, разрабатывают новые концепции, инструменты и API. А в ближайшем будущем Google и вовсе будет учитывать основные показатели производительности в поисковой выдаче.
Пользователям нравятся отзывчивые интерфейсы, а бизнесу — прибыльные проекты. И если производительность играет в этом не последнюю роль, то почему бы не заняться ее оптимизацией?
Наверное, любой разумный человек хоть раз в жизни спрашивает себя о чем-то из списка:
Этот пост — короткая памятка о том, что я делаю сам. Вся серия постов (если она вообще последует) будет отвечать на все актуальные вопросы современности, связанные с регулярным созданием контента, то есть на все актуальные вопросы современности вообще.
Кроме того, я спросил, какое оборудование используют коллеги из подкастов «Разбор Полётов», «devSchacht», «Podlodka Podcast», «Витая пара», и поделился этой информацией между строк. И это причина, по которой этот пост попал в хабы JavaScript и Разработка мобильных приложений — вероятно, кому-то может быть интересно узнать, чем пользуются их любимые подкастеры.
Совсем недавно Руслан (наш Генерал Маркетинг, ARG89) спросил, есть ли у меня список вещей, которые нужно взять с собой в путешествие на конференцию. Такого списка нет — есть только субъективное ощущение того, чем можно пожертвовать вот из этого:
В прошлый раз я хотел пожертвовать макбуком, например. Какая логика довела до жизни такой — читайте под катом.
Всем привет, меня зовут Семен Левенсон, я работаю teamlead’ом на проекте «Поток» от Rambler Group и хочу рассказать о нашем опыте использования Apollo.
Объясню, что такое «Поток». Это автоматизированный сервис для предпринимателей, позволяющий привлекать клиентов из Интернета в бизнес, не вовлекаясь в рекламу, и быстро создавать простые сайты, не являясь экспертом в верстке.
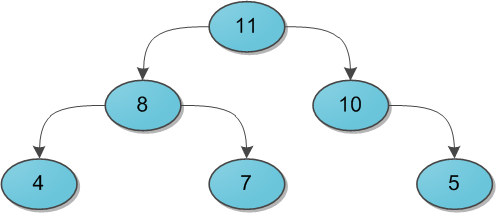
На заметку сразу скажу, что совершенно не обязательно думать про кучу исключительно как структуру, у которой родитель больше, чем его потомки. Никто не запрещает взять противоположный вариант и считать, что родитель меньше потомков — главное, выберите что-то одно для всего дерева. Для нужд этой статьи гораздо удобнее будет использовать вариант со знаком «больше».