Часть 0: Фракталы в простых числах.
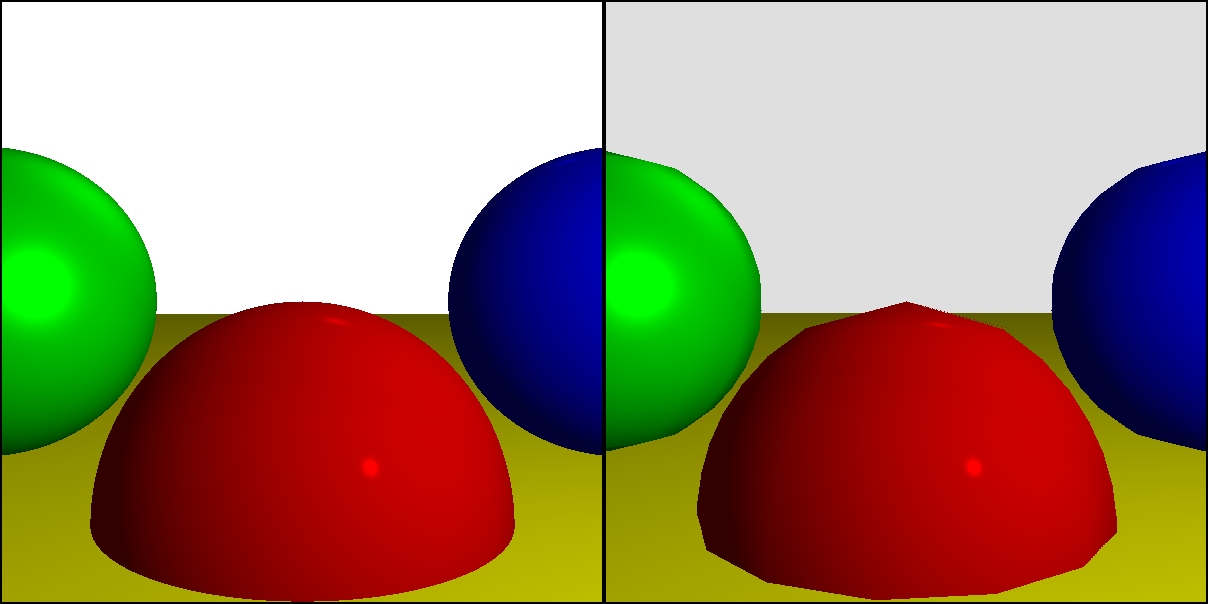
Часть 1: Фракталы в иррациональных числах.



В статье присутствуют Gif и контрастные картинки. У эпилептиков может случиться эпилептический припадок.

Статья является продолжением моей первой статьи «Фракталы в простых числах».

Следующая статья: Фракталы в иррациональных числах. Часть 2.



В предыдущей статье мы научились рисовать самоподобные паттерны с помощью взаимно простых чисел. В этой статье покажу фрактальную природу числа $$.
Без предисловия. Под кат.

Еще со времен обучения в университете я использовал LaTeX для оформления лабораторных и курсовых работ. Познакомился впервые с LaTeX на Coursera, на курсе "Документы и презентации в LaTeX".

В этой заметке я расскажу, как я писал диплом с помощью LaTeX и почему я использовал GitHub, Docker и TravisCI.

Привет, Хабр! К Дню знаний мы поговорили с победителями и обладателями золотых медалей на 59-й Международной Математической Олимпиады в Румынии: Станиславом Крымским и Владимиром Петровым. Кстати вот задачи с этого чемпионата, попробуйте решить.

Что компьютеру сделать легко, а что почти невозможно? Эти вопросы лежат в основе вопроса вычислительной сложности. Представляем вам карту этого ландшафта.

Различные классы сложности сортируют задачи в иерархическом виде. Один класс может содержать все задачи другого, плюс задачи, требующие дополнительных вычислительных ресурсов.

Какова фундаментальная сложность задачи? Такова постановка базовой задачи специалистов по информатике, пытающихся рассортировать задачи по т.н. классам сложности. Это группы, содержащие все вычислительные задачи, требующие не более фиксированного количества вычислительных ресурсов – таких, как время или память. Возьмём простой пример с большим числом типа 123 456 789 001. Можно задать вопрос: является ли оно простым числом – таким, которое делится только на 1 и себя? Специалисты по информатике могут ответить на него при помощи быстрых алгоритмов – таких, что не начинают тормозить на произвольно больших числах. В нашем случае окажется, что это число не является простым. Затем мы можем задать вопрос: каковы его простые множители? А вот для ответа на него быстрого алгоритма не существует – только если использовать квантовый компьютер. Поэтому специалисты по информатике считают, что две этих задачи относятся к разным классам сложности.

Сеточные системы координат, в которых плоскость делится на одинаковые симметричные элементы — на квадраты, треугольники, шестиугольники, достаточно известны. Им соответствуют квадратная, треугольная, шестиугольная симметрия. Но еще существует симметрия десятиугольная.

В ней плоскость не делится на десятиугольники, вместо этого все линии расположены под углами кратными 36°. Координаты в этой системе можно записывать целыми числами, по два целых числа на горизонтальное и вертикальное направление.



Расскажу как это нарисовать.

Задача о хроматическом числе плоскости формулируется следующим образом: в какое наименьшее число цветов можно раскрасить плоскость так, чтобы любые две точки на расстоянии 1 были покрашены в различные цвета?

Эту задачу сформулировали Хуго Хадвигер и Пал Эрдёш в сороковых годах XX века. Независимо от них примерно в то же самое время этой задачей занимались Эдуард Нелсон и Дж. Р. Исбелл. После работы Хадвигера 1961 года об открытых на тот момент проблемах, хроматическое число плоскости стало активно изучаться.

Сразу же было показано, что в 3 цвета плоскость требуемым образом раскрасить нельзя, однако 7 цветов достаточно. Действительно, легко выбрать на плоскости несколько точек так, что некоторые из них находятся на расстоянии ровно 1 (такая конструкция точек называется графом единичных расстояний), и затем перебором показать, что в 3 цвета эти точки раскрасить невозможно. Примеры таких графов — веретено Мозера и граф Голомба приведены на картинке ниже. Чтобы показать, что 7 цветов достаточно, замостим плоскость правильными шестиугольниками со стороной 0.4 и закрасим их по определённому паттерну, как на картинке ниже. Тогда, как несложно убедиться, концы любого отрезка длины 1 будут лежать в разных шестиугольниках различных цветов.



Однако, с тех пор никто не мог уточнить ни верхнюю, ни нижнюю границы. Задача получила название Проблема Нелсона — Эрдёша — Хадвигера. Прошло 60 лет, и вот, в апреле 2018 года математик-любитель Обри де Грей предъявил граф единичных расстояний, который нельзя покрасить в 4 цвета.

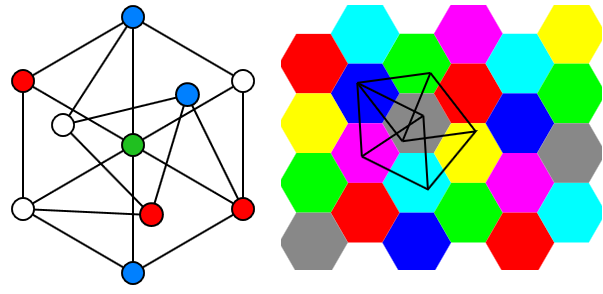
Всем привет.

В последнее время я работаю с распределенными системами и часто встречаюсь с проблемами работы с данными, части которых могут находиться в различных местах. Ну и так как я уже продолжительное время пишу на Haskell, описание проблемы и мощная система типов здорово помогли в дальнейшем развитии этой идеи. Речь пойдет о том, как всего одна несущая алгебраическая конструкция позволила решить задачу рециркулирующих данных в общем виде.

По мере копания в принципах управления компанией рано или поздно натыкаешься на две большие формации — Инквизицию и Ост-индскую торговую компанию. Про первое я не готов дискутировать во избежание холиваров, а вот про второе немного раскопал.

Это бизнес, который внезапно стал больше Англии, повлиял на технический прогресс, развязал пару войн и перебил сотни тысяч людей. На половине планеты следы этой компании — от «Садов Компании» близ мыса Доброй Надежды до упоминаний в современных фильмах вроде «Пиратов Карибского моря». Бизнес впечатлял.

Представьте ситуацию: вторая половина шестнадцатого века, в Англии полная задница с финансами. Народ бухтит и не повинуется, отлаженная судебная система стала жёстким рандомом, угроза войны, никаких надёжных внешних союзов. Понятно, что всё это приведёт к ещё большим проблемам, внутреннему расколу и гражданской войне. Надо было что-то делать, и делать довольно быстро.

Первый способ решения проблемы был прост как полено — перекредитоваться и зализать раны, а потом медленно отдавать занятое. Но вот только Амстердам давал под 14% в месяц, и поэтому слегка окосевшие от голландской наглости англичане брать отказались.

Оставалось думать. Это было непривычно, поэтому результат тоже получился неожиданный.

Как пронумеровать все двоичные деревья? Как на КДПВ: “дерево” из одного листа будет первым, дерево из двух листов вторым, второе дерево с ещё одной веткой, исходящей из корня – третьим. А как найти номер произвольного дерева в такой схеме?

Осознав, что я давно не писал на Хабр ничего полезного о ФП и Haskell, и что имеется вполне отличный повод для технической статьи, — решил тряхнуть стариной. Речь в статье пойдет о Software Trasactional Memory (STM), которую мне удалось реализовать на Free-монадах при участии ADTs (Algebraic Data Types) и MVars (конкурентные мутабельные переменные). И, в общем-то, Proof of Concept оказался крайне простым, в сравнении с «настоящим» STM. Давайте это обсудим.

Software Transactional Memory

Время от времени мне встречаются вопросы по математике, которые в каком-то смысле можно назвать «грамматически неверными».

Пример. «Интервал $$ является замкнутым или открытым?»
Пример. «Является ли $$ группой?»
Пример. «Каков ряд Фурье для $$?»

А вот ещё более глупые примеры.

Пример. «Является ли прямоугольник простым?»
Пример. "$$?"
Пример. «Каков ряд Фурье для пустого множества?»

Объединяет все эти примеры то, что они являются ошибками типизации: это попытки применения некого математического процесса к математическому объекту, который никак не может быть входными данными для него. Если для ответа на эти вопросы вы попытаетесь написать программу на каком-нибудь высоко математическом языке программирования, то она (я надеюсь!) не скомпилируется.

Математические объекты обычно не воспринимаются явно как имеющие типы в том же смысле, что и объекты в языках программирования с системой типов. Предполагается, что обычная математика должна формализироваться в системе Цермело — Френкеля (ZF), возможно, с аксиомой выбора, а в ZF каждый математический объект конструируется как множество. В этом смысле все эти объекты имеют одинаковый тип. (В частности, вопрос "$$" вполне логичен в ZF! И это одна из причин, по которой стоит не любить ZF в качестве основы для математики.) Однако, мне кажется, что на практике математические объекты неявно воспринимаются, как имеющие типы, и такой образ мышления математики усваивают, но не часто обсуждают.

Эта история началась с короткой статьи в New York Times о Люке Робитейле, 13-летнем школьнике из Юлесса, штат Техас, который выиграл Raytheon Mathcounts National Competition, правильно ответив на следующий вопрос:

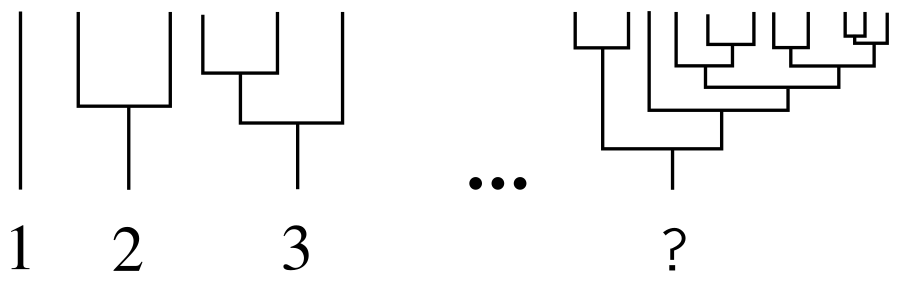
В амбаре кружком сидят 100 кур. Каждая из кур случайным образом клюёт свою ближайшую соседку слева или справа. Каково ожидаемое количество кур, которых никто не клюнул?

Судя по статье Times, Робитейлу потребовалось на ответ меньше секунды.

На следующий день Джордан Элленберг твитнул такую задачу:


«100 кур сидят в круге. Каждая клюёт случайным образом R или L. Клюнутые куры никого не клюют. Итерации проводятся до тех пор, пока не останется двух соседних неклюнутых кур. Сколько кур осталось?»

Мне не нужно умещать эту историю в 140 символов, поэтому я дополню вопрос Элленберга подробностями так, как я его понял. Исходная задача относилась к одной итерации синхронизированного случайного клевания, а теперь у нас есть несколько итераций. Во время одной итерации каждая курица случайным образом поворачивается влево или вправо и клюёт одну из своих соседок. Однако если курицу уже клюнули, она больше никогда не клюёт, даже её продолжают клевать. Если две соседние курицы клюют друг друга в одной итерации, обе они вылетают из игры на все последующие раунды. Если неклюнутая курица оказывается между двумя клюнутыми, её уже никогда не клюнут и поэтому она может клевать бесконечно. Вопрос заключается в том, какая часть кур выживет и станет «неуязвимыми»?

Ниже представлены спойлеры, так что сейчас вы можете попробовать ответить на вопрос сами. Пока вы этим занимаетесь, я немного поговорю о курах и о риторике и семиотике математических «текстовых задач».

Всем доброго!

У нас на этой неделе практически юбилей — стартует пятая группа "Разработчик Java", а это значит, что мы снова делимся всякими полезностями.

Поехали.

Если вы хотите убедиться, что вы переопределяете правильным образом, взгляните на это руководство, которое описывает различные средства, имеющиеся в вашем распоряжении, и некоторые подводные камни, которых следует остерегаться.

Дочерний класс может переопределить методы экземпляра своего родительского класса. Это называется переопределением метода. Сигнатура (тип возврата, тип параметров, количество параметров и порядок параметров) должна быть такой же, какой была определена в родительском классе. Переопределение метода выполняется для достижения полиморфизма во время выполнения программы.

Недавно коллега задал привычные уже вопросы про «зачем ходить на конференции» и «зачем смотреть записи на YouTube». Так как это друг, а не просто какой-то произвольный человек, захотелось ответить более обстоятельно, детально и по чесноку. К сожалению, в режиме онлайн, при живом общении, сделать это сложно: просто не упомнишь всех подробностей. С другой стороны, это отличная тема для хабрапоста: можно один раз написать развёрнутый обзор и потом, как истинный социофоб, отвечать на все вопросы ссылками на Хабр.

Идея проста: надо взять наиболее популярные доклады с JPoint 2017, кратенько пересказать, о чём там речь, почему это круто и зачем нужно лично мне. Каждый из этих докладов заслуживает отдельного разбора, но вначале — краткий обзор первой десятки. Поехали!

Пабло Пикассо в своей студии на фоне картины «Кухня», фотография Херберта Листа.

Художник и простота

Одни из самых любимых мной работ Пабло Пикассо — это его линейные рисунки. Он изобразил на некоторых из них животных: сову, верблюда, бабочку и т.д. Эта работа под названием «Собака» висит на моей стене:


(Можете перейти к интерактивному демо, в которой мы воссоздали «Собаку» с помощью представленных в статье математических расчётов)

Эти рисунки чрезвычайно просты, но каким-то образом им удаётся глубоко тронуть зрителя. Они создают впечатление простоты композиции и реализации. Одно движение руки и подпись создают настоящий шедевр! Рисунок одновременно кажется и небрежной импровизацией, и точно подобранной увертюрой в симфонии изящества.

Джеймс Тэнтон разбрасывается задачками по теории чисел с той же щедростью, с которой Джон Д. Рокфеллер раздавал десятицентовики. Я уже писал об одной из задач Тэнтона. Спустя несколько недель моё внимание привлёк этот твит о факториалах и квадратах и уже не давал мне покоя:


«4!+1 = 25, квадрат числа. 5!+1 = 121, тоже квадрат числа. Можете привести ещё один пример? Ещё два примера?»

С помощью ручки и бумаги легко показать, что $$ не подходит. Факториал $$ — это $$; прибавив $$, получим число $$, которое не является квадратом. (Оно раскладывается на множители как $$.) С другой стороны, $$ равно $$, а прибавив $$, мы получим $$, что равно $$. Это даёт нам очень милое уравнение:

Первая часть статьи может быть доказательством того, что трассировщики лучей — это изящный пример программного обеспечения, позволяющий создавать потрясающе красивые изображения исключительно с помощью простых и интуитивно понятных алгоритмов.

К сожалению, эта простота имеет свою цену: низкую производительность. Несмотря на то, что существует множество способов оптимизации и параллелизации трассировщиков лучей, они всё равно остаются слишком затратными с точки зрения вычислений для выполнения в реальном времени; и хотя оборудование продолжает развиваться и становится быстрее с каждым годом, в некоторых областях применения необходимы красивые, но в сотни раз быстрее создаваемые изображения уже сегодня. Из всех этих областей применения самыми требовательными являются игры: мы ожидаем рендеринга отличной картинки с частотой не менее 60 кадров в секунду. Трассировщики лучей просто с этим не справятся.

Тогда как это удаётся играм?

Ответ заключается в использовании совершенно иного семейства алгоритмов, которое мы исследуем во второй части статьи. В отличие от трассировки лучей, которая получалась из простых геометрических моделей формирования изображений в человеческом глазе или в камере, сейчас мы будем начинать с другого конца — зададимся вопросом, что мы можем отрисовать на экране, и как отрисовать это как можно быстрее. В результате мы получим совершенно другие алгоритмы, которые создают примерно похожие результаты.

Эта статья разделена на две основные части, Трассировка лучей и Растеризация, в которых рассматриваются два основных способа получения красивых изображений из данных. В главе Общие концепции представлены некоторые базовые понятия, необходимые для понимания этих двух частей.

В этой работе мы сосредоточимся не на скорости, а на чётком объяснении концепций. Код примеров написан наиболее понятным образом, который не обязательно является самым эффективным для реализации алгоритмов. Есть множество способов реализации, я выбрал тот, который проще всего понять.

«Конечным результатом» этой работы будут два завершённых, полностью рабочих рендереров: трассировщик лучей и растеризатор. Хотя в них используются очень отличающиеся подходы, при рендеринге простой сцены они дают схожие результаты:

Чёрные дыры могут переварить всё, что есть во Вселенной, но процесс извлечения из них информации пока остаётся недоступным

Если верить Google, то Стивен Хокинг – самый известный из живых физиков, а его самая известная работа – информационный парадокс чёрных дыр. Если вы знаете хоть что-то по поводу физики, вот, что вам необходимо узнать. До Хокинга чёрные дыры не представляли собой парадокса. Да, если вы бросите книжку в ЧД, вы больше не сможете её прочесть. Поскольку до того, что пересекло горизонт событий ЧД, уже нельзя дотянуться снаружи. Горизонт событий – замкнутая поверхность, внутри которой поймано всё, даже свет. Поэтому информация никак не вырвется из ЧД, книга пропала. Это неприятно, но физиков это не волнует. Информацию из книги, возможно, и не увидеть, но ничего парадоксального в этом нет.