Sergey Pshenichnikov, Tatiana Sotnikova
ALGEBRA OF MUSICAL TEXT
Sergey Pshenichnikov, Tatiana Sotnikova
Trio Sapiens
Musical text can be represented using matrix units, like the description of verbal texts and other symbolic sequences. In the future, mathematical recognition, and creation of musical sense with substantive justification for intermediate calculations (as opposed to AI) may become possible.
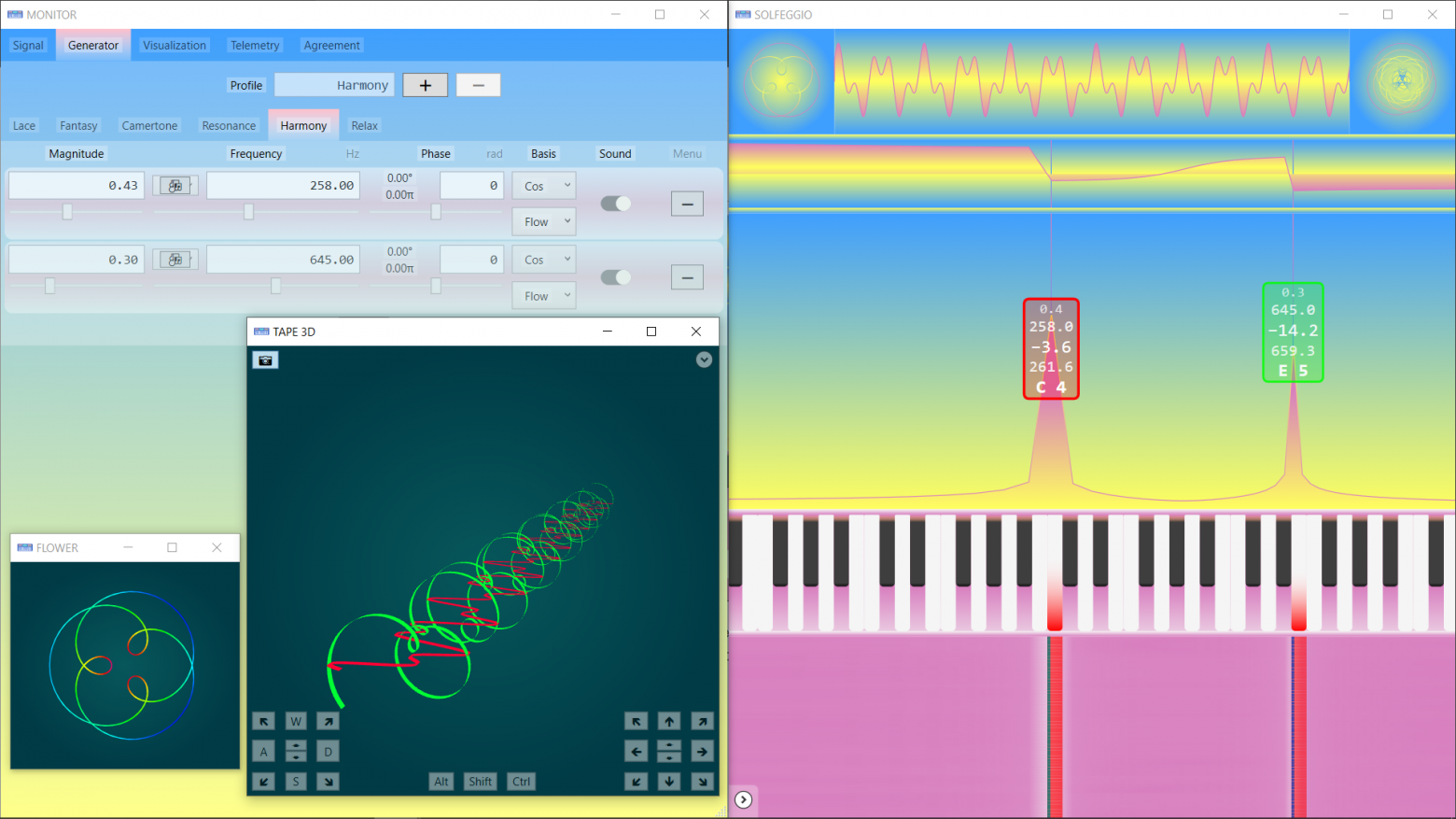
Sound has four properties: pitch, duration, volume, and timbre. Timbre is not considered yet. The dictionary of the algebra of musical texts is built on the basis of musical notation for the piano.
The duration here, for the sake of brevity of the first presentation, is considered as «absolute». «Relative» is not considered, although intervals are very well studied, and their features will be needed to categorize composers.
The complexity of the musical text for the application of mathematics is explained by the desire to simplify the reading of musical notes by musicians and to minimize the use of lower and upper additional lines.
To apply text algebra to musical symbolic sequences there is no need to use a five-line staff. What is useful and familiar to musicians is «unbearably harmful» for the use of algebra. It seems advisable to use a one-line staff. In this case, the musical text becomes like the verbal text.
To solve the problem, you need to find a transformation of the canonical musical text into a «thread». And as always, for a new application of algebra, correct coordination of the subject area is necessary. In this case, each used musical notation and symbol of modern musical notation must be assigned its own serial number (natural number).
Instead of a sign, you can use the names of each note symbol - then it will be a verbal notation of musical texts written in one line «thread»).
Since the musical scale is completely represented by piano keys, the first section in height of the dictionary of musical texts consists of 88 numbered white and black keys (of which 52 are white). This eliminates the need for an octave division of the scale, octave transfer signs, keys, five alteration signs (key and random), diatonic and chromatic semitones.
All notes of the scale became fundamental in algebraic musical notation. There is an order of magnitude more of them of them than the main stages of Guido Aretinsky, but the alteration signs and names of octaves disappeared, the use of which made musical texts algebraically incompatible with verbal texts. Numbers from 1 to 88 in algebraic notation constitute a fragment of the pitch dictionary for the «thread» one-line staff.
Numbering (coordination) of notes is needed to become in the future indices of mathematical objects (matrix units), which will replace the signs of notes or their names. These matrix units are binary generalizations of integers (hyperbinary numbers). The operation of division with remainder is defined for them, as for integers. The operation will allow you to divide musical texts and their f