На немецком «эйнштейн» звучит как «один камень». Один - «ein», камень - «Stain». Всем известно, что под этой фамилией жил один замечательный человек, и звали его ... Но в статье речь не о нём. Речь о математической задаче по поиску одной плитки, такой чтобы составленная из неё мозаика была непериодической. «Один камень» - это про плитку. В мозаике Пенроуза таких плиток две, а хотелось бы возможности использовать только одну. Не вдаваясь в детали можно сказать, что задача одной плитки в этом году (2023) решена. Получены интересные красивые мозаики.
Сначала была найдена «шляпа эйнштейна» - плитка, похожая на шляпу. Или, по моему скромному мнению, на рубашку. Из неё можно сделать отличную непериодическую мозаику. Только, для построения используются как сами шляпы, так и их зеркальные отражения. Считать ли это одной плиткой? Можно и не считать.
Дальше была найдена плитка «черепаха». Из неё тоже можно сложить непериодическую мозаику, по тем же самым правилам. Эти два вида плиток могут, плавно меняя форму, переходить друг в друга, меняя размер граней и при этом не меняя их направление. Ещё можно сложить непериодическую мозаику одновременно из этих двух плиток. Дальше больше. У такого плавного преобразования существует средний вариант, в котором длина граней одинакова.
Оказалось, такая мозаика, в которой есть одновременно и шляпы и черепахи, при обмене формой в момент, в котором длина граней становится одинаковой, составлена из плиток полностью одинаковой формы. То есть, существует ещё одна непериодическая мозаика, в которой плитка используется уже без своего зеркального отражения. Плитка, у которой грани модифицированы так, что она позволяет только непереодическое сложение названа «Spectre» (призрак). Задача решена, теперь уже точно.



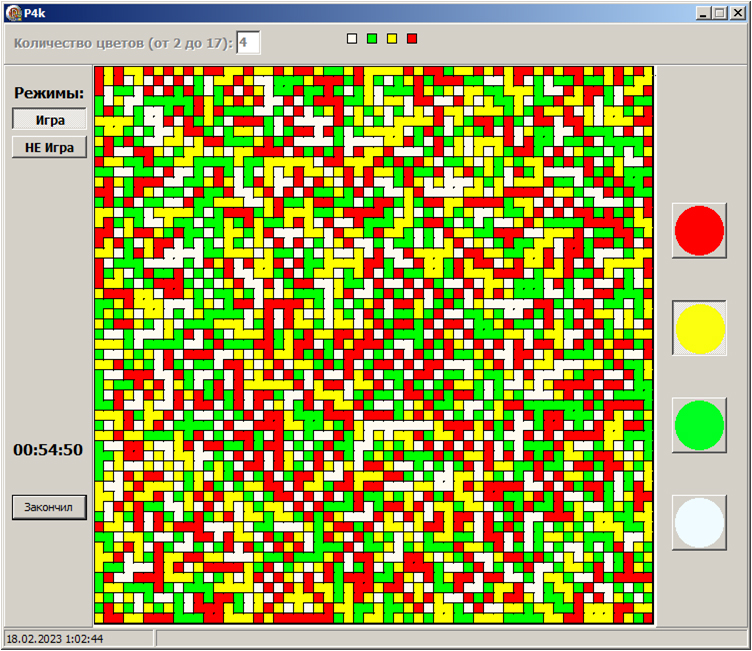
 Так получилось, что за последние полгода мне удалось познакомиться с несколькими простыми (в смысле правил) и в чем-то схожими настольными играми. Первым в этом ряду был «Сет», потом «Барабашка», а уже летом мы играли в «Доббль». Сразу скажу, что все перечисленные игры весьма увлекательные, однако, речь в этом посте пойдет, конечно же, не об этом. Дело в том, что спустя некоторое время (другими словами, наигравшись) меня заинтересовали идеи, лежащие в основе этих игр, и которые оказались тесно связанными именно с комбинаторикой. В данном посте речь пойдет о самой простой (на мой взгляд) игре — «Барабашке», которая, кстати, в оригинальном варианте имеет более благозвучное название «Geistesblitz» (нем. — озарение).
Так получилось, что за последние полгода мне удалось познакомиться с несколькими простыми (в смысле правил) и в чем-то схожими настольными играми. Первым в этом ряду был «Сет», потом «Барабашка», а уже летом мы играли в «Доббль». Сразу скажу, что все перечисленные игры весьма увлекательные, однако, речь в этом посте пойдет, конечно же, не об этом. Дело в том, что спустя некоторое время (другими словами, наигравшись) меня заинтересовали идеи, лежащие в основе этих игр, и которые оказались тесно связанными именно с комбинаторикой. В данном посте речь пойдет о самой простой (на мой взгляд) игре — «Барабашке», которая, кстати, в оригинальном варианте имеет более благозвучное название «Geistesblitz» (нем. — озарение).