Подделываем вашу подпись при помощи шарнирного механизма. Теорема Кемпе


Царица всех наук


Я люблю давать простые задачки студентам на лекции. Во-первых, понятно, скольких мы потеряли, во-вторых, это переключение из режима потребления информации в режим выдачи результатов, в третьих — возможность проявить себя для шустрых. Сплошные плюсы!
Одна из простых задач звучит так: «При переводе картинки из цветового пространства RGB в YUV мы выполняем прореживание, то есть выкидываем каждый четный столбец и каждую четную строку в компонентах U и V (все компоненты пикселя по 1 байту). Вопрос: во сколько раз меньше данных у нас стало?» Эта операция называется chroma subsampling и широко используется при сжатии видео, например.
Забавно, что когда-то давно, когда винчестеры были меньше, а дискеты больше, студенты реально отвечали на этот вопрос быстро. А в последние годы регулярно народ в ступор впадает. Приходится разбирать по частям: «Если выкинуть каждую четную строку и каждый четный столбец, во сколько раз меньше данных будет у компоненты?» Почти хором: «В четыре». Начинаю подкалывать: «Отлично! У нас было 3 яблока, первое осталось как есть, а от второго и третьего осталось по четвертинке. Во сколько раз меньше яблок у нас стало?» Народ ржет, но, наконец-то, дает правильный ответ (заметим, не все).
Это было бы смешно, если бы от способности быстро в уме прикинуть результат не зависела способность быстрее создавать сложные алгоритмы.
И хорошо видно, как эта способность в широких массах студентов заметно плавно падает. Причем не только в нашей стране. Придуман даже специальный термин: «цифровое слабоумие» ("digital dementia") — снижение когнитивных способностей, достаточно серьезное, чтобы повлиять на повседневную деятельность человека.
Кому интересно как теряют мозг студенты масштабы бедствия и что с этим делать — добро пожаловать под кат!


Существуют три вида лжи: ложь, наглая ложь и статистика (источник)
 13 июня 1944 года, через неделю после вторжения союзников в Нормандию, громкий жужжащий звук прогремел в небе избитого боями Лондона. Источником звука было недавно разработанное немецкое орудие войны: воздушная бомба V-1. Будучи предшественником крылатых ракет, V-1 была самоходной бомбой, управляемой с помощью гироскопов, питалась она от простого пульсирующего воздушно-реактивного двигателя, который поглощал воздух и воспламенял топливо 50 раз в секунду. Такая высокая частота пульсации давала бомбе характерный звук, зарабатывая ей прозвище «жужжащая бомба» (в оригинале – «buzz bomb» – прим. перев.).
13 июня 1944 года, через неделю после вторжения союзников в Нормандию, громкий жужжащий звук прогремел в небе избитого боями Лондона. Источником звука было недавно разработанное немецкое орудие войны: воздушная бомба V-1. Будучи предшественником крылатых ракет, V-1 была самоходной бомбой, управляемой с помощью гироскопов, питалась она от простого пульсирующего воздушно-реактивного двигателя, который поглощал воздух и воспламенял топливо 50 раз в секунду. Такая высокая частота пульсации давала бомбе характерный звук, зарабатывая ей прозвище «жужжащая бомба» (в оригинале – «buzz bomb» – прим. перев.).
Давайте ненадолго перенесёмся в школьные годы и вспомним уроки математики и физики. Помните, чему равно число π? Естественно, помните, мы же на Хабре! А чему равно π в квадрате? Это тоже странный вопрос. Конечно, 9,87. А чему равно ускорение свободного падения g помните? Ещё бы, это число так тщательно вдолбили в нашу память, что захочешь — не забудешь: 9,81 м/c². Конечно, оно может варьироваться, но для решения базовых школьных задачек мы обычно использовали именно это значение.
А теперь, внимание, следующий вопрос: а с какого это перепугу π² примерно равно g?

В прошлом году я написал программу, вычисляющую 255 цифр числа π на самом первом микропроцессоре от Intel - 4004. В той статье я упоминал рекорд ENIAC'a - 2035 цифр [^1], но побить его не смог. Настало время закрыть гештальт. В этот раз возьмём одного из преемников от Intel - 4040.
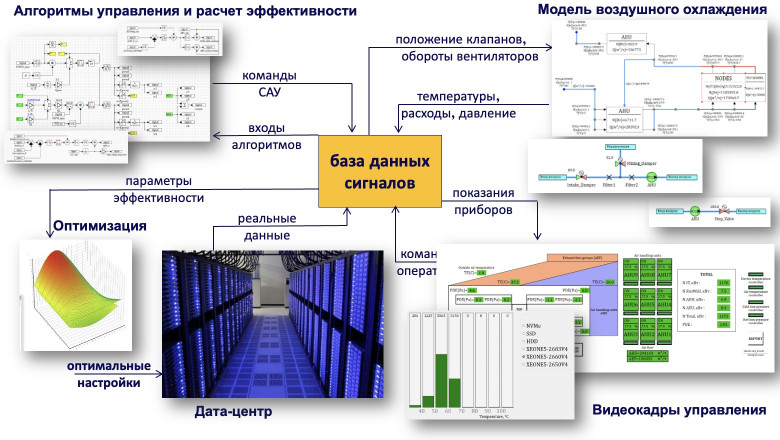
Все знают, что Россия — энергетическая сверхдержава, она же – «разорванная в клочья Обамой бензоколонка». Но не все знают, как это может отражаться в области развития математического моделирования. Расскажу одну жизненную историю.
Начну с далекого 2007 года. Довелось мне в те времена поработать на крупном заводе, который «эффективные менеджеры» как раз делили на несколько отдельных предприятий, каждое из которых крутилось, как могло. В том цеху, который и стал одним из таких предприятий, на токарных станках могла крутиться (и крутилась!) металлическая болванка размером с автобус. А в печку для нагрева металла можно было затолкать паровоз. Целиком. Когда я в первый раз увидел токарный станок, на котором крутится и обтачивается деталь размером с автобус, моему восторгу не было предела. Гордость за страну переполняла до состояния «в зобу дыханье сперло». А потом старожилы показали ту часть цеха, где стояли фундаменты таких же станков и пояснили:
- А вот тут были станки для точной обработки. Их продали китайцам по цене металлолома.
- А почему вот другие не продали?
- Потому, что у них точность обработки такая, что их только в металлолом можно сдать. Поэтому они здесь работают и крутятся как могут, и обтачивают валы турбин Siemiens.
Схема бизнеса был гениальна: Siemiens привозил на завод многотонные болванки, их неделями и месяцами обтачивали до состояния заготовок и увозили для чистовой обработки в Германию. Где уже выполняли чистовую доводку на точных и дорогих станках. Главные затраты при черновой обработке – это износ станков и инструмента, зарплата токаря и электроэнергия, необходимая для вращения тонн металла. Поскольку электроэнергия в РФ дешевле немецкой, недели обработки болванок с лихвой окупают транспортировку, а низкая точность обработки не требует дорогого обслуживания и мало чувствительна к износу еще советского оборудования. В итоге весь бизнес заключался в «перепродаже» дешевой электроэнергии из РФ в Германию, но в виде металлических обточенных болванок.
 В этой статье я расскажу об одном необычном подходе к генерации лабиринтов. Он основан на модели Амари́ нейронной активности коры головного мозга, являющейся непрерывным аналогом нейронных сетей. При определенных условиях она позволяет создавать красивые лабиринты очень сложной формы, подобные тому, что приведен на картинке.
В этой статье я расскажу об одном необычном подходе к генерации лабиринтов. Он основан на модели Амари́ нейронной активности коры головного мозга, являющейся непрерывным аналогом нейронных сетей. При определенных условиях она позволяет создавать красивые лабиринты очень сложной формы, подобные тому, что приведен на картинке. Различные реализации игры «Жизнь» описывались на Хабре уже неоднократно. В этой статье, в качестве продолжения этой темы, рассматривается ещё один её вариант: в качестве игрового поля используется регулярная решётка на плоскости Лобаческого. Описываются общие методы использования плоскости Лобачевского в программах и необходимые для этого математические приёмы.
Различные реализации игры «Жизнь» описывались на Хабре уже неоднократно. В этой статье, в качестве продолжения этой темы, рассматривается ещё один её вариант: в качестве игрового поля используется регулярная решётка на плоскости Лобаческого. Описываются общие методы использования плоскости Лобачевского в программах и необходимые для этого математические приёмы.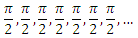
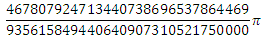
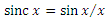 (ну и 1 при x = 0, хотя неважно). Тогда каждый член ряда — это значение следующего интеграла в цепочке:
(ну и 1 при x = 0, хотя неважно). Тогда каждый член ряда — это значение следующего интеграла в цепочке:



Однажды, выполнив в Гугле запрос "Three body problem" ("Задача трёх тел"), я был просто поражен - первая страница результатов состояла только из ссылок на роман китайского писателя-фантаста Лю Цысиня с соответствующим названием, а также на телесериал, снятый по этому роману, т.е. ссылок на собственно задачу трёх тел не было вообще! Мне это показалось удивительным и несправедливым, поскольку сама по себе задача трёх тел тоже может выглядеть увлекательной в популярном изложении. В этой публикации я постарался привести некоторые доказательства этого утверждения.
 Но нам был интересен обратный вопрос, как, имея, например, изображение сердечка, получить выражение для функции, графиком которой будет это самое сердечко.
Но нам был интересен обратный вопрос, как, имея, например, изображение сердечка, получить выражение для функции, графиком которой будет это самое сердечко.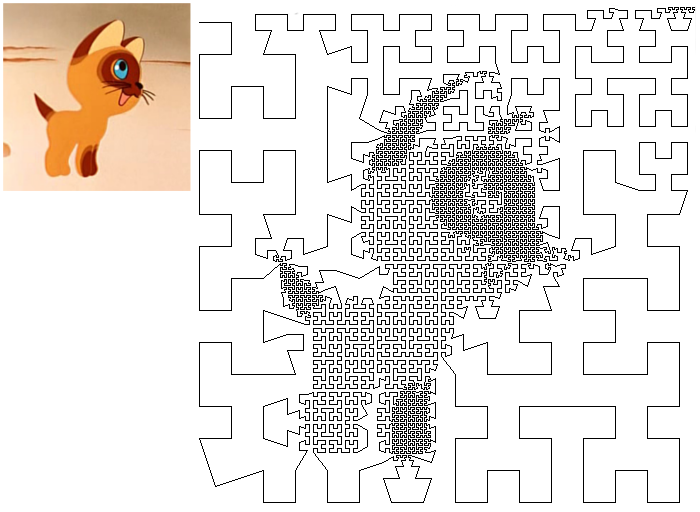

[Прим. пер.: на Хабре уже был перевод этой статьи, но незавершённый примерно на четверть.]
Неправда.
Калькулятор должен показывать результат введённого математического выражения. А это намно-о-ого сложнее, чем кажется.
В этом посте я расскажу величайшую историю о разработке приложения-калькулятора.
На изображении выше показан калькулятор из iOS.
Заметили что-нибудь?
Он посчитал неправильно.
(10100) + 1 − (10100) равно 1, а не 0.
Android считает правильно. А причина, по которой он это делает, абсолютно безумна.
