Сейчас я вам что покажу, закачаетесь. Обязательно загляните под кат, самые интересные картинки я припрятал там.
Я продолжаю рассказ о применении философской геометрии на практике.
Прошлая часть была обзорная, она говорила о том, что многие века геометрия использовалась для поиска универсальных идеальных законов природы. Эти законы повсеместно использовались в произведениях искусства, архитектуре и духовной жизни.
Сегодня я расскажу про замечательную пропорцию «корень из трех». Я покажу ее сакральный смысл, а под катом продемонстрирую пример из современного дизайна, который повергнет вас в шок ;)
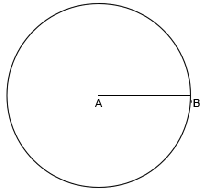
Начнем с построения пропорции. Возьмем отрезок AB.

Примем его за радиус и построим окружность с центром в A.
Теперь построим вторую окружность с тем же радиусом, но с центром в B.
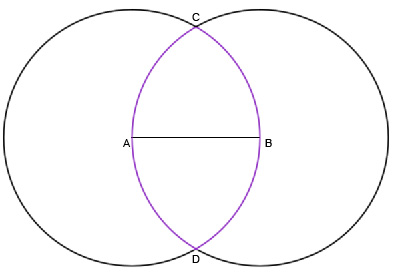
У нас получилась фигура ACBD, имеющая огромное значение для наших предков. Она называется Vescica Piscis (пузырь рыбы). Самый простой и важный пример — она давно является символом христианства.
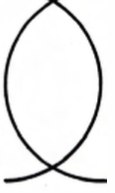
Я продолжу под катом. Спорим, никогда не догадаетесь чем там все закончится :)



 В математике чрезвычайно редко случается, чтобы учёный старше 40 лет опубликовал первую серьёзную научную работу. Ещё реже бывает, чтобы эта работа имела большую научную ценность. Именно
В математике чрезвычайно редко случается, чтобы учёный старше 40 лет опубликовал первую серьёзную научную работу. Ещё реже бывает, чтобы эта работа имела большую научную ценность. Именно 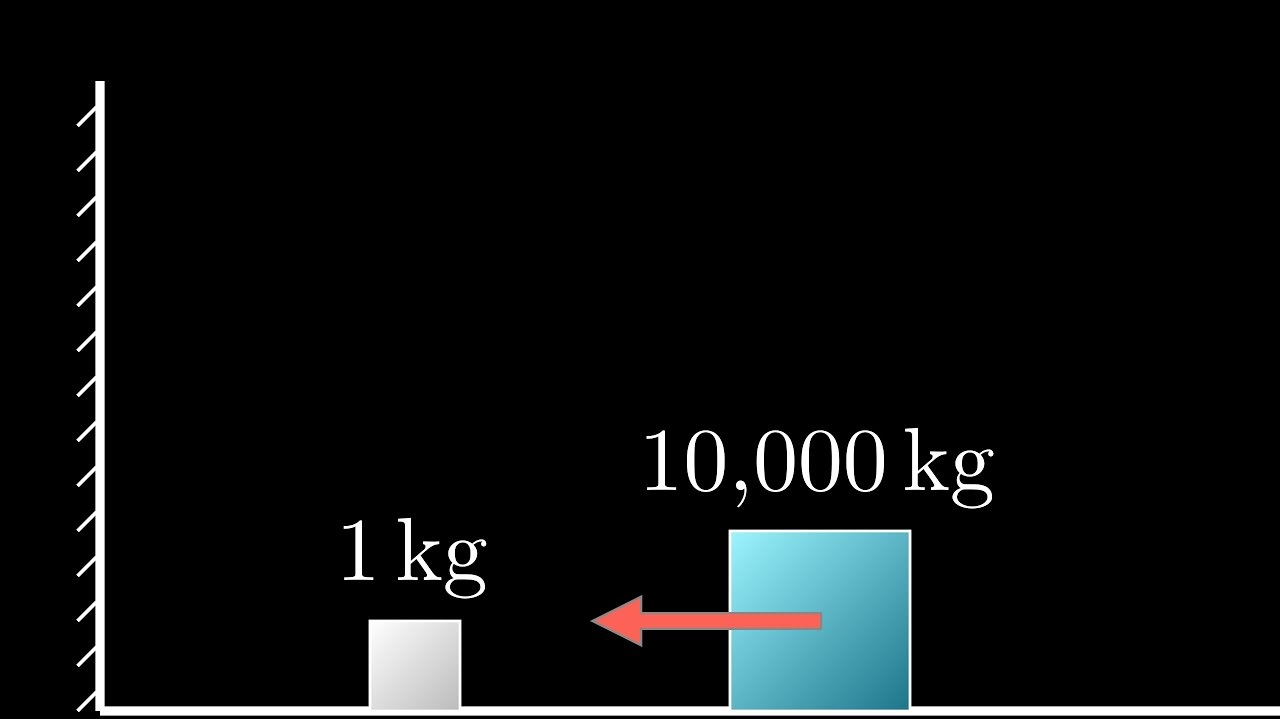









 (с) xkcd
(с) xkcd