Вышла недавно статья на Хабре о том, как можно самому создать на функциональном языке такие структуры как Очередь (первый зашёл, первый вышел) и Дек (напоминает двусторонний стек — первый зашёл, первый вышел с обоих концов). Посмотрел я на этот код и понял, что он жутко неэффективен — сложность порядка O(n). Быстро сообразить, как создать структуры с O(1) у меня не вышло, поэтому я открыл код библиотечной реализации. Но там была не лёгкая и понятная реализация, а <много кода>. Это было описание пальчиковых деревьев, необходимость и элегантность которых для этой структуры данных хорошо раскрывается текущей статьёй.
Пальчиковые деревья
В этой статье мы рассмотрим пальчиковые деревья. Это функциональные неизменяемые структуры данных общего назначения, разработанные в работе Гинце и Паттерсона. Пальчиковые деревья обеспечивают функциональную структуру данных Последовательность (
sequence), которая обеспечивает амортизированной доступ постоянный во времени для добавления как в начало, так и в конец последовательности, а также логарифмическое время для конкатенации и для произвольного доступа. В дополнение к хорошему времени асимптотических исполнения, структура данных оказывается невероятно гибкой: в сочетании с моноидальными тегами на элементах, пальчиковые деревья могут быть использованы для реализации эффективных последовательностей с произвольным доступом, упорядоченных последовательностей, интервальных деревьев и очередей приоритетов.
Статья будет состоять из 3-х частей:
Пальчиковые деревья (Часть 1. Представление)
Пальчиковые деревья (часть 2. Операции)
Пальчиковые деревья (Часть 3. Применение)
Разрабатывая структуру данных
Основа и мотивация пальчиковых деревьев пришла от 2-3 деревьев. 2-3 деревья — это деревья, которые могут иметь две или три ветви в каждой внутренней вершине и которые имеют все свои листья на одном и том же уровне. В то время, как бинарное дерево одинаковой глубины
d должны быть 2
d листьев, 2-3 деревья гораздо более гибкие, и могут быть использованы для хранения любого числа элементов (количество не должно быть степенью двойки).
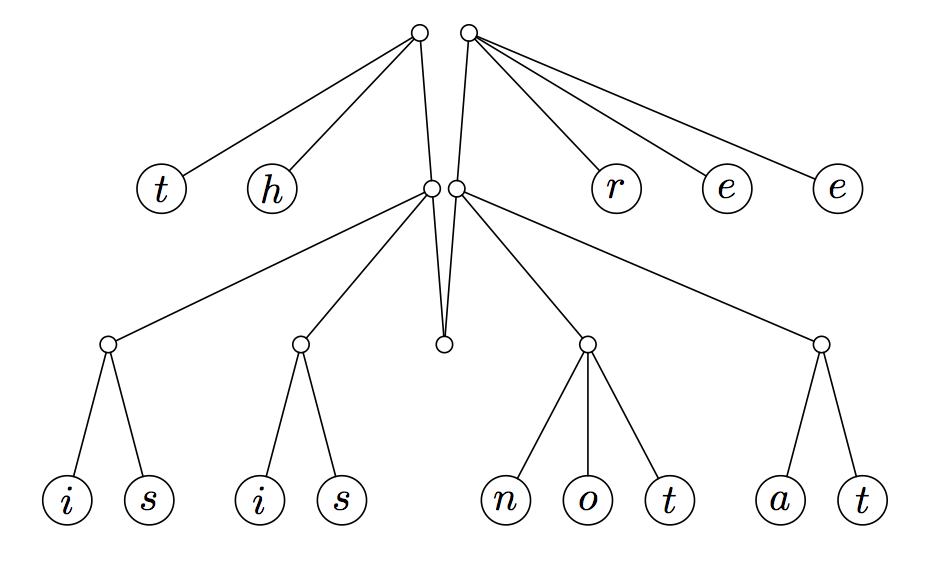
Рассмотрим следующее 2-3 дерево:

Это дерево хранит четырнадцать элементов. Доступ к любому из них требует трех шагов, и если бы мы должны были добавить больше элементов, количество шагов для каждого из них будет расти логарифмически. Мы хотели бы использовать эти деревья для моделирования последовательности. Тем не менее, во многих применимых последовательностях очень часто и неоднократно обращаются к началу или к концу, и гораздо реже к середине. Для удовлетворения этого пожелания, мы можем изменить эту структуру данных так, чтобы приоритет доступа к началу и к концу был наивысшим в отличие от других особенностей.
В нашем случае, мы добавляем два пальца. Палец просто точка, в которой вы можете получить доступ части структуры данных, в императивных языках это было бы просто указателем. В нашем случае, однако, мы будем реструктуризовать всё дерево и сделаем родителей первых и последних детей двумя корнями нашего дерева. Визуально, рассматривая вопрос об изменении дерева выше, захватываем первый и последний узлы на предпоследнем слое, и тянем их вверх, позволяя остальной части дерева свисать:

 Атака на башни Всемирного Торгового Центра 11 сентября 2001 года унесла жизни 658 сотрудников финансовой компании Cantor Fitzgerald. Ее директор Говард Лутник, потерявший в тот день родного брата, столкнулся с невиданной ранее проблемой. И дело было даже не в том, что серверы компании, включая резервные, также были погребены под обломками. Информация частично была доступна, но она была закрыта за сотнями учетных записей погибших коллег. На помощь были привлечены специалисты из компании Microsoft, они задействовали мощные серверы для максимально быстрого брутфорса — от доступа к данным зависело существование компании, и надо было успеть к первому открытию торгов после атак. Ускорить взлом могли персональные данные погибших. Лутнику пришлось обзванивать родственников и, в самый неподходящий момент, задавать им серию вопросов: день свадьбы, название колледжа или университета, имя собаки.
Атака на башни Всемирного Торгового Центра 11 сентября 2001 года унесла жизни 658 сотрудников финансовой компании Cantor Fitzgerald. Ее директор Говард Лутник, потерявший в тот день родного брата, столкнулся с невиданной ранее проблемой. И дело было даже не в том, что серверы компании, включая резервные, также были погребены под обломками. Информация частично была доступна, но она была закрыта за сотнями учетных записей погибших коллег. На помощь были привлечены специалисты из компании Microsoft, они задействовали мощные серверы для максимально быстрого брутфорса — от доступа к данным зависело существование компании, и надо было успеть к первому открытию торгов после атак. Ускорить взлом могли персональные данные погибших. Лутнику пришлось обзванивать родственников и, в самый неподходящий момент, задавать им серию вопросов: день свадьбы, название колледжа или университета, имя собаки. 






 Опять на собеседованиях по Java спрашивают про
Опять на собеседованиях по Java спрашивают про 
