Оглавление (на данный момент)
Часть 1. Описание, операции, применения.
Часть 2. Ценная информация в дереве и множественные операции с ней.
Часть 3. Декартово дерево по неявному ключу.
To be continued...
Очень сильное колдунство
После всей кучи возможностей, которые нам предоставило декартово дерево в предыдущих двух частях, сегодня я совершу с ним нечто странное и кощунственное. Тем не менее, это действие позволит рассматривать дерево в совершенно новой ипостаси — как некий усовершенствованный и мощный массив с дополнительными фичами. Я покажу, как с ним работать, покажу, что все операции с данными из второй части сохраняются и для модифицированного дерева, а потом приведу несколько новых и полезных.
Вспомним-ка еще раз структуру дерамиды. В ней есть ключ
x, по которому дерамида есть дерево поиска, случайный ключ
y, по которому дерамида есть куча, а также, возможно, какая-то пользовательская информация
с (cost). Давайте совершим невозможное и рассмотрим дерамиду… без ключей x. То есть у нас будет дерево, в котором ключа x нет вообще, а ключи y — случайные. Соответственно, зачем оно нужно — вообще непонятно :)
На самом деле расценивать такую структуру стоит как декартово дерево, в котором ключи x все так же где-то имеются, но нам их не сообщили. Однако клянутся, что для них, как полагается, выполняется условие двоичного дерева поиска. Тогда можно представить, что эти неизвестные иксы суть числа от 0 до
N-1 и
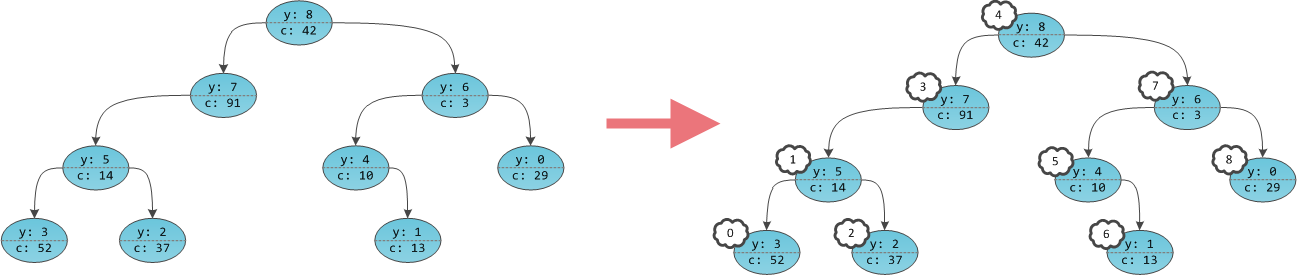
неявно расставить их по структуре дерева:
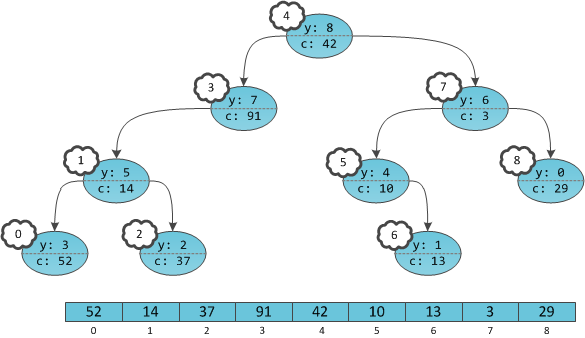
Получается, что в дереве будто бы не ключи в вершинах проставлены, а сами вершины пронумерованы. Причем пронумерованы в уже знакомом с прошлой части порядке in-order обхода. Дерево с четко пронумерованными вершинами можно рассматривать как массив, в котором индекс — это тот самый неявный ключ, а содержимое — пользовательская информация
c. Игреки нужны только для балансировки, это внутренние детали структуры данных, ненужные пользователю. Иксов
на самом деле нет в принципе, их хранить не нужно.
В отличие от прошлой части, этот массив не приобретает автоматически никаких свойств, вроде отсортированности. Ведь на информацию-то у нас нет никаких структурных ограничений, и она может храниться в вершинах как попало.

 В мире всегда существовали некоторые закрытые общества, которые доступны только ограниченному кругу людей. Для того, чтобы попасть туда нужно было обладать чем-то необычным. Например, ездить на
В мире всегда существовали некоторые закрытые общества, которые доступны только ограниченному кругу людей. Для того, чтобы попасть туда нужно было обладать чем-то необычным. Например, ездить на 

 У любого желающего писать программы для продукции фирмы Apple в жизни наступает такой момент, когда ему приходиться изучить новый язык программирования — Objective-C. Когда-то этот счастливый момент постиг и меня. А чтобы лучше запомнить основные особенности этого языка, решил законспектировать свои мысли во время осмысления его документации, которыми и делюсь с вами.
У любого желающего писать программы для продукции фирмы Apple в жизни наступает такой момент, когда ему приходиться изучить новый язык программирования — Objective-C. Когда-то этот счастливый момент постиг и меня. А чтобы лучше запомнить основные особенности этого языка, решил законспектировать свои мысли во время осмысления его документации, которыми и делюсь с вами.