Практические сложности настройки устройств Modbus TCP/RTU в промышленной среде и легкое решение через мобильное приложение.

Когда заходит речь о писателях в стиле киберпанк, имя Брюса Стерлинга всегда заслуженно идет через запятую с Уильямом Гибсоном, Нилом Стивенсоном и другими. Вместе с тем, есть такое ощущение, что идеи Стерлинга были восприняты массовой культурой в гораздо меньшей степени.

Это интересно, так как с точки зрения технологических предсказаний Стерлинг намного опередил и Гибсона, и других коллег — да и вообще был и остается не столько литератором, сколько серьезным мыслителем-футурологом.

Рассмотрим повнимательнее идеи и творчество одного из главных технофантастов XX века.

Попробую на маленьком примере показать откуда берётся запутанный код.

Получаем задание от менеджера, для простоты это будет просто логическая функция. И пытаемся написать лучший код.

Для упрощения написания маленькая буква будет означать что условие ложно, а большая — что истинно.

Представляем функцию в виде карты Карно, чтобы оптимизировать всё что можно:

Я не математик, но люблю решать задачи. Я люблю трудные задачи, которые не знаешь, как решать, а если и знаешь, трудно написать код верно.

Наконец, все работает. Остаются черновики, которые выбросить жалко. Выброшу лишнее с черновика и оставлю конспект, который и через годы напомнит решение.

Говорят "У человека феноменальная память - он помнит все". Он записывает. Не помните, что делали три дня назад? Ведите дневник, а не покупайте "таблетки для памяти".

Это третья часть обзора и она всё также вводная)). В первой было рассказано о категориях типов, а во второй — о категории подкатегорий типов с её морфизмами-функторами. В этот же раз нам предстоит разобраться, как эти самые функторы взаимодействуют между собой.

Когда я решил написать программу для простой цифровой фотосъёмки на Apple II, то думал использовать камеры Quicktake. Выбор казался очевидным, потому что это были камеры Apple, способный подключаться к компьютеру через последовательный порт.

Объём задачи немного расширился, когда мне удалось декодировать фотографии Quicktake 100: захотелось научиться декодировать фотографии Quicktake 150 и Quicktake 200. Из-за этого пришлось погрузиться в тему обработки изображений глубже, чем мне хотелось изначально. В этой статье я расскажу о том, как мне удалось заставить работать декодер Quicktake 150 с достаточно приемлемой скоростью на процессоре 6502 с частотой 1 МГц.

Формат Quicktake 150 проприетарный и не имеет документации, однако в проекте dcraw существуют свободные программные декодеры. Они стали моим фундаментом для создания первого декодера на Apple II. К сожалению, они написаны на C, крайне плохо задокументированы и чрезвычайно непонятны (для меня). Сжатие выполняется при помощи кода Хаффмана с переменной длиной (то есть используется битовый сдвиг), а для воссоздания изображения требуется большой объём 16-битных вычислений. Со всем этим 6502 справляется плохо.

Но для начала мне нужно было переписать исходный алгоритм так, чтобы он работал с полосами по 20 пикселей (из-за ограничений памяти). Я написал функциональный декодер, и он работал идеально, но... для декодирования одной фотографии требовалось семьдесят минут.

Студенты пришли в библиотеку, чтобы подготовиться к экзаменам. Всего у них предметов. Каждая из книг покрывает некоторое множество предметов. Нужно выбрать минимальное число книг, которые покроют все предметы.

Характеризация — одна из интересных головоломок игры Puzzle Hunt Сиднейского университета 2010 года. Ее сюжет в том году был основан на произведениях Льюиса Кэрролла «Приключения Алисы в Стране чудес» и «Алиса в Зазеркалье». Игра состояла из множества сцен, которые представляли собой импровизации на знаменитое «Безумное чаепитие». Каждая сцена содержала одну головоломку, органично встроенную в повествование. Характеризация была последней головоломкой игры перед финальным мета-заданием и имела пять «звезд» по сложности из пяти.

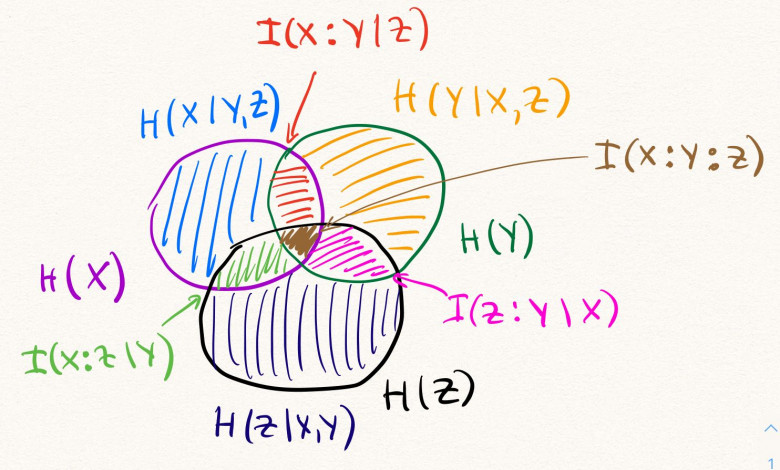
Мы ежедневно работаем с информацией из разных источников и поэтому имеем интуитивные представления о том, что означает, когда один источник является более информативным, чем другой. Однако далеко не всегда понятно, как это правильно определить формально. Не всегда большое количество текста означает большое количество информации. Например, среди СМИ распространена практика, когда короткое сообщение из ленты информационного агентства переписывают в большую новость, но при этом не добавляют никакой «новой информации». Или другой пример: рассмотрим текстовый файл с романом «Война и мир» в кодировке UTF-8. Его размер — 3.2 Мб. Сколько информации содержится в этом файле? Изменится ли это количество, если файл перекодировать в другую кодировку? А если заархивировать? Сколько информации вы получите, если прочитаете этот файл? А если прочитаете его второй раз?

По мотивам открытой лекции для Computer Science центра рассказываю о том, как можно математически подойти к определению понятия "количество информации".

Вам это может показаться странным, но были времена, когда отрицательные числа казались людям чем-то неестественным, причём даже тем людям, которые зарабатывали себе на жизнь числами — математикам. Как можно считать числом то, что не имеет физического воплощения? С отрицательными числами в итоге смирились, но уж что точно невозможно было терпеть, так это совсем непонятную величину, квадрат которой, это уже противоречит всякому здравому смыслу. Тем не менее время показало, что законы физики и математики, сформулированные с использованием имеют больший смысл, чем законы, сформулированные без неё. Еще в 19 веке Карл Фридрих Гаусс отметил, что "Если бы вместо того, чтобы называть +1, −1,​ положительной, отрицательной или мнимой (или даже невозможной) единицей, их назвали бы, скажем, прямой, обратной или боковой единицей, то едва ли можно было бы говорить о какой-либо темноте".

В статье хочу рассказать о том, как небольшой математический трюк, придуманный для решения кубических уравнений 500 лет назад, вошёл в фундамент современной науки и инженерии.

Отладка больших CMake-проектов часто превращается в боль. Уходит не один час на то, чтобы с помощью message() и бубна найти проблему. Но существуют более удобные и эффективные способы. Например, отладчик, который позволяет пошагово пройтись по CMake-скриптам и посмотреть значение переменных. Или профилировщик, показывающий последовательность вызовов и время их выполнения. Как их использовать? Читайте в статье.

Стивен Вольфрам — британский физик, математик и программист. Уже более 20 лет он разрабатывает свою версию «Теории всего», которая раньше вызывала в основном критику и несогласие, а сегодня становится всë более популярной.

Приветствую тебя, читатель, меня зовут Вадим Бельский, и я уже больше полугода делаю свою небольшую 4-x стратегию MyCivGame, вдохновленную играми Civilization и Total War. Сейчас я расскажу тебе, как устроен мир в нашей любимой игре Civilization, и мы с тобой вместе подумаем, можно ли сделать его лучше (а самое главное, нужно ли это)!

Книга «Реальная криптография» за авторством Дэвида Вонга является весьма любопытным литературно-теоретический гибридом «упрощенного учебника по криптографии» (первая половина книги) и «реального положения дел» (вторая половина книги).

Автор позиционирует книгу как практическое руководство для широкого круга читателей, предпринимая попытки уйти от классического и набившего оскомину шифра Цезаря и прочих исторических моментов, обещая читателю актуальные примеры, рекомендации и криптографические «рецепты».

В 1876 году Питер Гатри Тейт предложил измерять то, что он называл «запутанностью» узлов. Шотландский математик, во многом предвосхитивший современную теорию узлов, искал практический способ отличать один узел от другого — задача, мягко говоря, непростая. 

Тейт предложил такой критерий различия. Разложим узел на плоскости и посмотрим на точки самопересечения. В одной из таких точек «перевернём» пересечение: мысленно разрежем, поменяем местами верхнюю и нижнюю нити и снова «склеим». Повторяя операцию столько раз, сколько нужно, можно получить незавязанный круг. Минимальное число таких «переворотов» он назвал мерой незавязанности — сегодня это известно как число развязывания узла.

В данной статье мы кратко рассмотрим, зачем создавать прототипы игр. Да, всё довольно просто, но не так очевидно, как кажется на первый взгляд. Теорию подкрепим кейсом прототипирования экономики 4х стратегии.

В этой статье мы напишем самую простую программу, исполним её одним из самых изощерённых способов, упакуем через велосипед, а потом велосипедом и запустим.

Больше ничего интересного не будет :-)

Прошлой зимой на встрече в финской глуши высоко за Полярным кругом собралась группа математиков, чтобы поразмышлять о судьбе математической вселенной. 

Было минус 20 градусов по Цельсию, и пока некоторые катались на лыжах, Хуан Агилера, специалист по теории множеств из Венского технического университета, предпочитал задерживаться в столовой, отрывая кусочки пуллы (традиционного финского сладкого хлеба) и обсуждая природу двух новых понятий бесконечности. Результаты, по мнению Агилеры, были грандиозными. «Мы просто пока не в состоянии их оценить», — сказал он. 

Бесконечность, как ни странно, существует во многих формах и размерах. Это известно с 1870-х годов, когда немецкий математик Георг Кантор доказал, что множество действительных чисел (всех чисел на числовой прямой) больше множества целых чисел, хотя оба множества бесконечны. (Коротко говоря: как бы вы ни пытались сопоставить действительные числа с целыми, вы всегда получите больше действительных чисел.) Эти два множества, утверждал Кантор, представляют собой совершенно разные типы бесконечности и, следовательно, обладают совершенно разными свойствами. 

Как фундаментальные физические ограничения спасают Вселенную от хаоса и делают её познаваемой?
Мы привыкли думать, что сложность мира делает его принципиально непредсказуемым. Но если это так, как вообще возможна наука, описывающая мир и делающая предсказания о его поведении? Но что, если фундаментальные ограничения нашей Вселенной не просто физические константы, а необходимое условие её существования? Они не только делают вселенную устойчивой, но позволяют нам понять её законы.

Эта статья показывает без этих "ограничений" Вселенная столкнулась бы с теоретической невычислимостью. Бесконечная скорость распространения информации и непрерывное пространство привели бы к бесконечному объему данных, необходимых для расчета даже одного шага эволюции системы. Причинно-следственные связи рухнули бы, сделав мир абсолютно непознаваемым и неустойчивым. Познаваемость Вселенной через законы физики и математические модели — не удача, а необходимость, вытекающая из её устройства. "Необоснованная эффективность математики" имеет под собой физическое обоснование.

На Хабре уже выходило множество статей о том, что наш мир — это симуляция. Но, несмотря на это, прошу дать мне шанс с этой статьёй, в которой мы рассмотрим фундаментальные вещи, к которым все давно привыкли и не подвергают сомнению, хотя они толсто намекают…

А также мы рассмотрим практический вопрос: что это может значить лично для нас, если симуляционная теория верна.