Пользователь
Задача трёх тел (не китайская нефантастика)

Однажды, выполнив в Гугле запрос "Three body problem" ("Задача трёх тел"), я был просто поражен - первая страница результатов состояла только из ссылок на роман китайского писателя-фантаста Лю Цысиня с соответствующим названием, а также на телесериал, снятый по этому роману, т.е. ссылок на собственно задачу трёх тел не было вообще! Мне это показалось удивительным и несправедливым, поскольку сама по себе задача трёх тел тоже может выглядеть увлекательной в популярном изложении. В этой публикации я постарался привести некоторые доказательства этого утверждения.
Насколько быстр Javascript? Симулируем 20 миллионов частиц

Я бросил себе вызов: симулировать 1000000 (миллион) частиц на чистом Javascript на телефоне, используя только CPU и добившись 60 FPS.
Поехали.
Задача не особо сложна, если выполнять всю работу на GPU, но правило гласит, что нужно пользоваться только CPU, при этом работая на JS, так что никакого WASM.
Квантовая концепция времени. Структура Мультивёрса: эмерджентные истории и потоки информации

С незапамятных времён люди используют специальные языковые конструкции, чтобы говорить о прошлом и будущем – ненаблюдаемых частях реальности, которые доступны нам лишь в памяти и воображении. Но только в 80-е гг. XX века учёные догадались, что другие времена – это разновидность других вселенных. Прошлое и будущее – альтернативные версии настоящего, которое объективно не может быть одним моментом. Отрицание реальности этих альтернатив и выделение какого-то особого момента «здесь и сейчас» является проявлением солипсизма и пространственно-временного шовинизма. Все моменты и все места одинаково реальны и образуют блочную мультивселенную, вне которой не существует точки отсчёта, позволяющей проследить её эволюцию во времени. И ничто, включая наше сознание, не может перемещаться из одного момента в другой или из одной вселенной в другую. Быть в моменте – значит быть там вечно. Примерно так можно описать концепцию времени в квантовой теории.
В данной статье я рассказываю о внутренней структуре Мультивёрса, которая в действительности гораздо сложнее, чем на популярных изображениях с ветвящимися деревьями параллельных миров. Параллельные вселенные интерферируют на микроскопическом уровне, разделяя между собой неотличимые экземпляры элементарных частиц, но образуют на макроскопических масштабах относительно автономные истории, в некотором приближении подчиняющиеся законам классической физики. Оказывается, развитие событий в каждой отдельной истории зависит от того, какие ещё истории есть поблизости. Поэтому амплитуды вероятностей в квантовой теории отражают объективную меру «толщины» ветвей универсальной волновой функции, а не знание наблюдателя о системе. Также мы пересматриваем традиционные представления о причинно-следственных связях и физическом детерминизме, даём многомировое объяснение двухщелевого эксперимента с отложенным выбором и обобщаем три разных определения энтропии.
Анимация фрактала Lozi map

Предыдущая статья натолкнула меня на мысль написать ещё одну программу, генерирующую последовательности изображений с другим типом фракталов. В ней пришлось применить более сложную анимацию коэффициентов.
Трансмировая идентичность: мультивёрсные двойники, границы «я», свобода воли и квантовое бессмертие

Спросите себя: кто я? А кого вы, собственно, спрашиваете? Почему я — это я, а не кто‑то другой? Я в прошлом и я в будущем — это всё ещё я, или уже не я? Что делает меня мной? Что нужно изменить в моём теле и в моей психике, чтобы я перестал быть собой? Что во мне остаётся неизменным в течение всей жизни? Могут ли разные люди думать одни и те же мысли? Могу ли я в одних и тех же обстоятельствах принимать разные решения? Если меня усыпить и создать идентичную копию, кем из двойников я себя осознаю, когда проснусь? Все эти вопросы обретают новый смысл с точки зрения многомировой интерпретации Эверетта, согласно которой у каждого из нас есть множество двойников в параллельных мирах. Вы никогда не знаете точно, кем из этих двойников являетесь и в каком мире находитесь. Означает ли это, что вам нужно переопределить своё «я» или полностью от него отказаться, заменив местоимением «мы»? В этой статье мы разбираем все вопросы, связанные с тождеством личности, самоидентичностью в Мультивёрсе, расщеплением наблюдателя и свободой воли. Также мы разоблачаем популярный миф о квантовом бессмертии.
PINN или нейросети, знающие физику

Что такое PINN и какова область их применения?
PINN появились сравнительно недавно (в 2019 году была опубликована работа Raissi), но уже активно применяются для некоторых задач физики. Отличительная особенность данных нейросетей состоит в том, что в Loss‑функцию включены невязки от уравнений, которые описывают рассматриваемый физический процесс. Вход такой нейросети — это координаты (пространственные или временные, в зависимости от задачи). И еще одна особенность — для обучения не требуется таргетов, так как, повторюсь, в Loss минимизируется отклонение предсказанных значений от уравнений.
Можно сказать, что PINN — это замена численному моделированию и тогда, возникает вопрос: «А нужны ли нейросети там, где хорошо работают численные методы». Но не все так просто. Представьте, что Вы или Ваш коллега провел эксперимент, например, измерил скорости частиц в потоке жидкости, или получил точечные измерения температуры. Если Вы действительно имеете опыт проведения эксперимента, наверняка знаете, что экспериментальные данные далеко не идеальны и могут принести много головной боли при обработке. А теперь представим, что все же Вы эту обработку провели, получили датасет из эксперимента, и теперь хотите эти данные использовать в уравнениях, чтобы получить другие параметры течения. Например, измерили скорость, а из уравнений гидродинамики, хотите получить давление. Или другими словами, провести ассимиляцию данных, говоря на современном околонаучным языком. Численное моделирование в таком случае можно дать сбой, потому что даже тщательно отфильтрованные данные могут быть шумными (особенно если от них требуется брать производные, а если еще и вторые, то совсем, шляпа). Или их может быть мало (например, температуру измеряли термопарой в нескольких точках). В данном случае, вроде, эксперимент есть и потенциально восстанавливать одни величины по другим можно, решая уравнения. И тут на помощь могут прийти PINN. Потому что они работают иначе, чем численные методы. Они не используют схем переноса, а параметры нейросети минимизируются в выбранных точках.
Циклические массивы
Во многих задачах, связанных с обработкой данных, возникает проблема нехватки памяти для их хранения.
Например, с датчика непрерывно поступают данные с частотой дискретизации F=1000 Гц, которые сохраняются в массиве. Однако, для анализа данных используется конечное временное окно наблюдения, например, T=10 секунд. Таким образом, при поступлении нового отсчета данных необходимы лишь последние N=T*F=10 000 значений.
Подобные задачи возникают при фильтрации сигналов, построении индикаторов для торговли на биржах, в нейронных сетях.
Как американская коррупция превратила физика-ядерщика в быдло-кодера

Это история из цикла «как войти в IT», написанная старпером, ветераном броуновского движения, который помнит динозавров. Поэтому его опыт вхождения в ИТ никому не пригодится, но представляет интерес с точки зрения истории.
Также поделюсь своим мыслями об интерфейсе инженерного ПО. Участвуя в разработках различного ПО, предназначенного для ускорения разработки сложных систем, периодически приходится выслушивать жалобы от новых пользователей на «кривой и устаревший» интерфейс ПО. Однако инженеры, погруженные в проблемы проектирования реальных железок, вообще не задают нам таких вопросов, либо потому, что уже искривили свои руки о кривой интерфейс, либо им это вообще неважно. Более того, есть два примера, когда реальные высокопрофессиональные инженеры в своей области предъявляли претензии обратного свойства, и первая версия кривая версия GUI была удобнее, а вот улучшения делали какие-то полупокеры.
К написанию данного текста меня подтолкнула беседа с одним из крутых разрабов из «жирной» конторы, с которым мы пересеклись на яхте в Средиземном море. Узнав, что я тоже из Бауманки, и у меня свой бизнес, он заинтересовался и выспрашивал. Как я смог начать бизнес на софте, почему не пошел в большую контору, типа Yandex, Сбер и прочие. У него тоже знакомство с софтом началось как создание собственной разработки по анализу результатов металлургических испытаний в лаборатории, но закончилось работой прогером по найму. Попивая вино на яхте где-то между Турцией и Грецией в 2023 году, он предположил, что, возможно, если бы он продолжал писать софт для металлургических исследований, то, наверное, сейчас мог плавать на своей яхте, а не арендованной, и не около Турции, а на Карибах (но это не точно). А поскольку фарш невозможно провернуть назад, я решил описать свою историю успеха, так как она забавна и поучительна.
Спектральный метод на примере простых задач матфизики

Метод конечных элементов своими руками
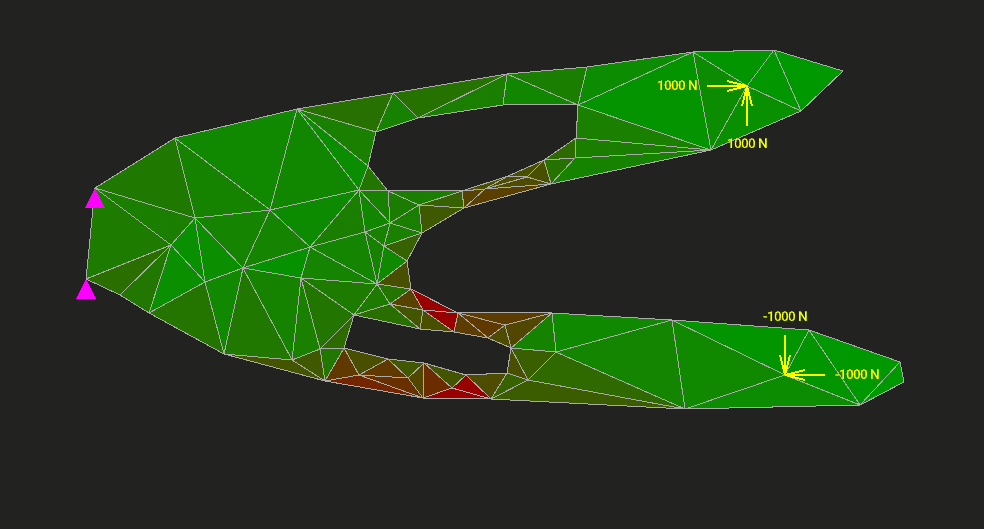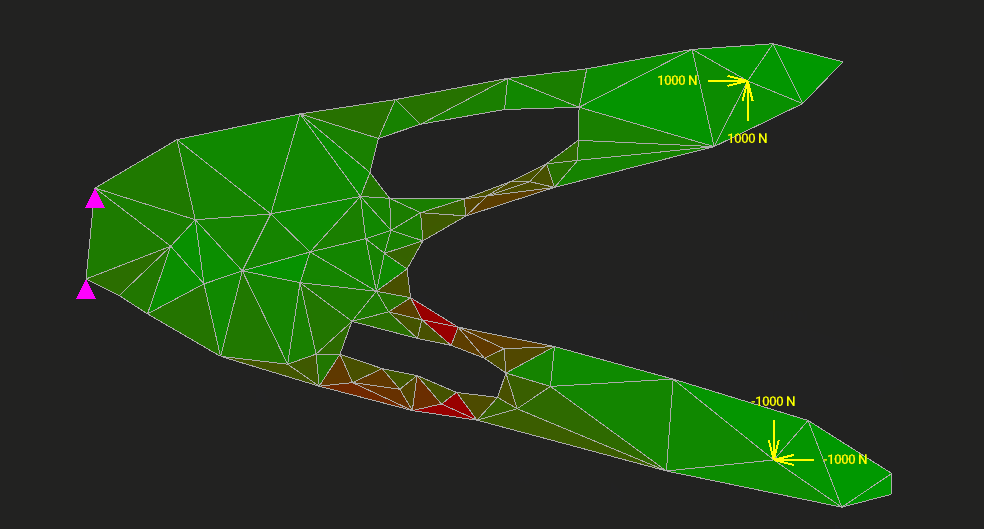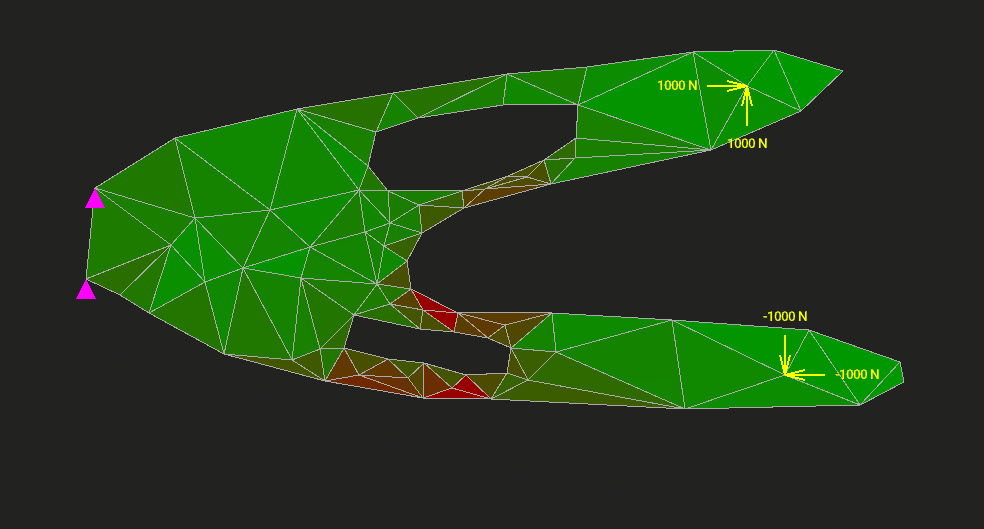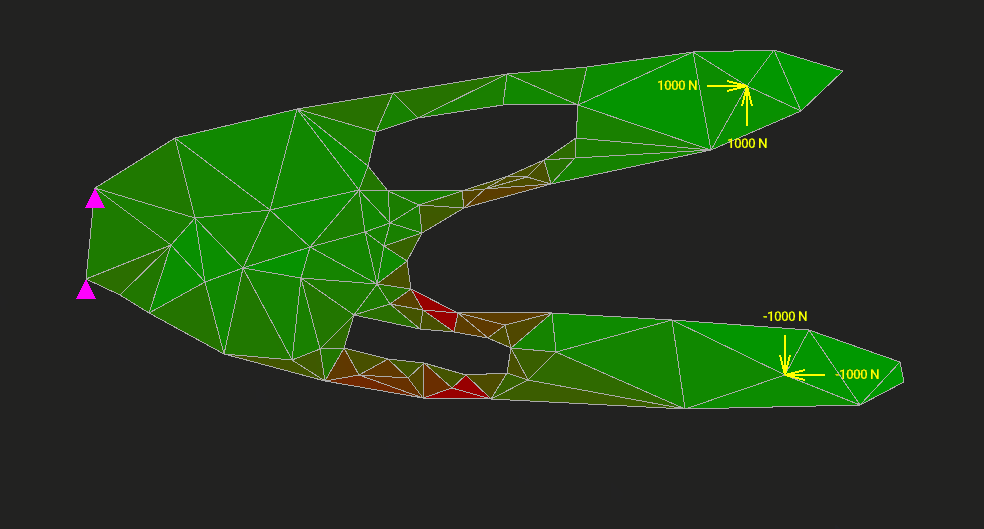
Метод конечных элементов (МКЭ) применяют в задачах упругости, теплопередачи, гидродинамики — всюду, где нужно как-то дискретизировать и решить уравнения сплошной среды или поля. На Хабре было множество статей с красивыми картинками о том, в каких отраслях и с помощью каких программ этот метод приносит пользу. Однако мало кто пытался объяснить МКЭ от самых основ, с простенькой учебной реализацией, желательно без упоминания частных производных через каждое слово.
Мы напишем МКЭ для расчёта упругой двумерной пластины на прочность и жёсткость. Код займёт 1200 строк. Туда войдёт всё: интерактивный редактор, разбиение модели на треугольные элементы, вычисление напряжений и деформаций, визуализация результата. Ни одна часть алгоритма не спрячется от нас в недрах MATLAB или NumPy. Код будет ужасно неоптимальным, но максимально ясным.
Размышление над задачей и написание кода заняли у меня неделю. Будь у меня перед глазами такая статья, как эта, — справился бы быстрее. У меня её не было. Зато теперь она есть у вас.
OpenFOAM с точки зрения программиста-физика
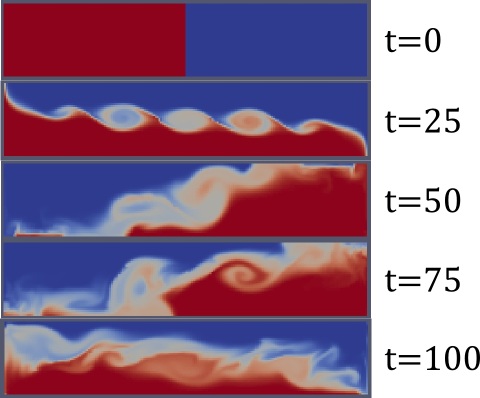
В компании Intel разрабатывается довольно много ПО для моделирования различных физических процессов. В некоторых из них мы используем пакет OpenFOAM, и в этом посте я постараюсь дать краткое описание его возможностей.
Что такое OpenFOAM? Это, пользуясь термином Википедии, открытая (GPL) платформа для численнного моделирования — в первую очередь для моделирования, связанного с решением уравнений в частных производных методом конечных объемов, и в самую первую очередь — для решения задач механики сплошных сред.
КПДВ: эволюция двух несмешивающихся жидкостей разной плотности, изначально разделенных тонкой перегородкой (пример «lockExchange» из стандартной поставки OpenFOAM). Переходные цвета обозначают ячейки сетки, где присутствует доля и той, и другой жидкости (более точно: при симуляции используется метод объёма жидкости).
Опыт работы с фильтром Калмана на примере NMEA данных
Цель статьи не в объяснении принципов Калмановского фильтра, а в его демонстрации на примере реальных (сырых) данных. Желающие могут модифицировать исходники и поэкспериментировать с алгоритмом, я надеюсь что моя работа поможет тем, кто столкнется с подобной задачей.
Используемые данные — c GPS-приемника в формате NMEA-0183, в часности сообщения GGA и VTG.
Фильтрация необходима по причине зашумленности GPS. Причины помех в GPS данных разные. Основные:
- атмосферные помехи.
- препятствия для сигнала.
- положение орбиты GPS. Например, невысокое наклонение орбит GPS (примерно 55°) серьёзно ухудшает точность в приполярных районах Земли.
Все это суммарно приводит к скачкам положения, смещениям курса, и прочим неприятностям. Причем в работе в первую очередь мне нужно было получить именно отфильтрованную скорость.
Дело в том что скорость, измеряемая оборудованием и передаваемая в сообщении VTG давала неправдоподобные показания (скачки и т. д.), которые крайне затрудняли задачи управления.
Поэтому было решено построить модель фильтр в Octave, и получив скорость как производную от GPS данных, представленных сообщением GGA, сравнить с оригинальными данными скорости из сообщения VTG.
Для удобства сравнения данные требуется вывести на один график.
С фильтрацией данных и их производных прекрасно справляется фильтр Калмана.
Применение фильтра для задач автопилота и курсовертикали является «классикой».
Объяснение фильтра Калмана в картинках
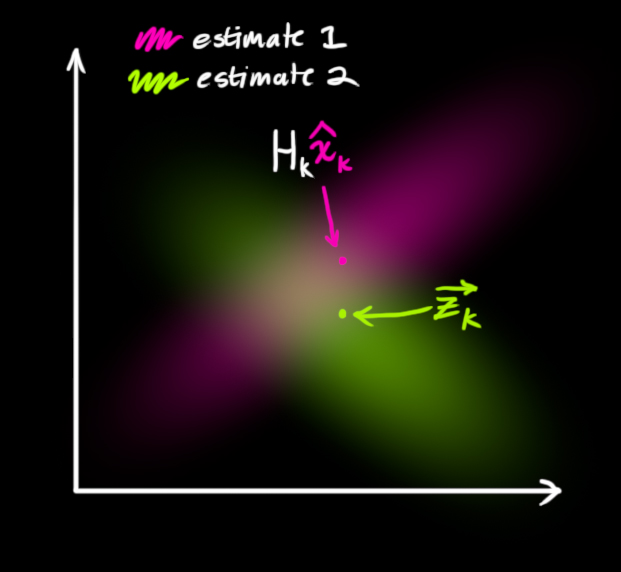
Я обязан рассказать вам о фильтре Калмана, потому что он выполняет просто потрясающую задачу.
Как ни удивительно, о нём, похоже, знают немногие разработчики ПО и учёные, и это печалит меня, потому что это очень обобщённый и мощный инструмент для объединения информации в условиях присутствия неопределённости. Иногда его способность извлечения точной информации кажется почти магической, а если вы думаете, что я слишком много болтаю, то взгляните на это видео, в котором я показываю, как фильтр Калмана определяет ориентацию свободно плавающего тела, посмотрев на его вектор скорости. Потрясающе!
Альфа-бета фильтр Калмана: фильтр «Hello, world!»

В статье описана реализация альфа-бета фильтра Калмана, приведено подробное его описание и программный код -- всё написано для новичков в этой сфере для того, чтобы помочь им начать свой путь и не отпугнуть от дальнейшего изучения методов фильтрации.
Фильтр Калмана — !cложно?
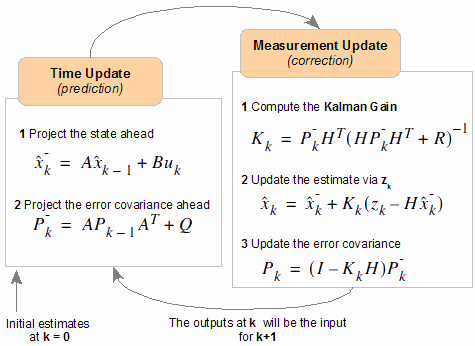 Недавно прочитал пост из «Дополненной реальности», в котором упоминается Фильтр Калмана в сравнении с более простым «альфа-бета» фильтром. Давно собирался сочинить нечто вроде сниппета по составлению ФК, и вот думаю самое время. В статье я вам расскажу как на практике можно составить расширенный ФК не особо утруждая себя высоконаучными размышлениями и глубокими теоретическими изысканиями.
Недавно прочитал пост из «Дополненной реальности», в котором упоминается Фильтр Калмана в сравнении с более простым «альфа-бета» фильтром. Давно собирался сочинить нечто вроде сниппета по составлению ФК, и вот думаю самое время. В статье я вам расскажу как на практике можно составить расширенный ФК не особо утруждая себя высоконаучными размышлениями и глубокими теоретическими изысканиями.Кратко о гидродинамике: теория устойчивости
В тексте будет написано ещё немножечко теории на примере задачи об устойчивости течения в плоском канале. Таких задач в реальности великое множество — в слоях и в ограниченных полостях разной формы, в слоях вертикальных, горизонтальных и наклонных, в обычной жидкости и пористой среде, в проводящей жидкости под влиянием магнитного поля и в растворе какой-нибудь соли под действием температуры, в полости под влиянием как угодно направленной вибрации, на границе раздела двух жидкостей… В общем, одно только перечисление всех подуровней гидродинамики может отнять пару часов, и то всё вспомнить вряд ли удастся. А также будет показано несколько примеров чисто гидродинамической неустойчивости течений, без влияния дополнительных факторов (изображения около 700 кбайт).
Предыдущие же посты были написаны, чтобы обеспечить математический и смысловой фундамент формул в дальнейших постах.
Кратко о гидродинамике: ты помнишь, как всё начиналось?
Кратко о гидродинамике: уравнения движения
Кратко о гидродинамике: сохранение энергии
Кратко о гидродинамике: сохранение энергии
Данный пост рассматривает законы сохранения энергии в идеальной и вязкой жидкости. Они заведомо необходимы для полноты описания движения, однако, в изотермическом случае теплообмена как такового нет, и потому для описания достаточно использовать уравнение Навье-Стокса и уравнение неразрывности. Надеюсь, этот пост будет последним из достаточно абстрактных постов, описывающих общую теорию и не практически привязанных к конкретным постановкам задач.
Предыдущие посты:
Кратко о гидродинамике: ты помнишь, как всё начиналось?
Кратко о гидродинамике: уравнения движения
Кратко о гидродинамике: уравнения движения
В нынешней публикации описаны основные уравнения движения идеальной и вязкой жидкости. По возможности кратко рассмотрен их вывод и физический смысл, а также описаны несколько простейших примеров их точных решений. Увы, этими несколькими примерами доступные аналитически решения уравнений Навье-Стокса в значительной мере исчерпываются. Напомню, что Институт Клэя отнёс доказательство существования и гладкости решений к проблемам тысячелетия. Гении уровня Перельмана и выше — задача вас ждёт.
Кратко о гидродинамике: ты помнишь, как всё начиналось?
Информация
- В рейтинге
- Не участвует
- Зарегистрирован
- Активность