
Статья про разработку системы управления робототехнического устройства на примере привода рулевой поверхности малогабаритной ракеты.

Математическое моделирование и одноимённый ЯП

Статья про разработку системы управления робототехнического устройства на примере привода рулевой поверхности малогабаритной ракеты.
Частой задачей при обучении теории автоматического управления является расчет корректирующего устройства методом желаемой ЛАЧХ. Эта задача дается для ознакомления с большим миром управления в частотной области.
Зачем вообще частотный метод, когда есть модальный?
Дело в том, что в 1978 году Джоном Дойлом в статье Guaranteed Stability Margins for LQG Regulators было показано, что для LQG регуляторов не существует гарантированного запаса устойчивости, и поэтому в зависимости от объекта управления, шума и помех в каналах управления и измерения, LQG регулятор может быть сколь угодно чувствительным к неопределенности в модели и временным задержкам, а значит он может быть сколь угодно не надежным (робастным).
В данной статье покажем несколько способов расчета компенсатора частотными методами, помимо метода желаемой ЛАЧХ, в пакете Matlab с использованием Control System Toolbox.

Продолжаем публикацию лекций по предмету "Управление в технических системах". Кафедра "Ядерные энергетические установки" МГТУ им. Н.Э. Баумана. Автор: Олег Степанович Козлов.
1. Введение в теорию автоматического управления.2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.
3. Частотные характеристики звеньев и систем автоматического управления регулирования. 3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено. 3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.
4. Структурные преобразования систем автоматического регулирования.
5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (САР).
6. Устойчивость систем автоматического регулирования. 6.1 Понятие об устойчивости САР. Теорема Ляпунова. 6.2 Необходимые условия устойчивости линейных и линеаризованных САР. 6.3 Алгебраический критерий устойчивости Гурвица. 6.4 Частотный критерий устойчивости Михайлова. 6.5 Критерий Найквиста.
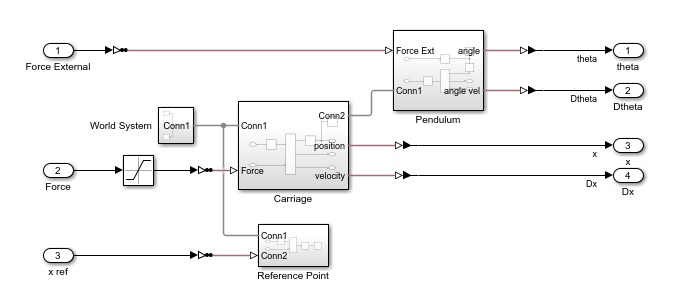
Простой и популярной реализацией закона управления обратным маятником является PID регулятор. Современные средства настройки коэффициентов PID регулятора позволяют решать подобные задачи нажатием пары кнопок даже без знания математики, физики и вообще без каких-либо технических знаний. Рассмотрим пример настройки PID регуляторов в Simulink для классического обратного маятника.
Объект управления (Plant)
Модель перевернутого маятника соберем в библиотеке Multibody. Для этого нам не понадобится знание физики и математики. Библиотека Multibody предоставляет нам готовые блоки степеней свободы, твердых тел, преобразований координат, которые нужно только верно соединить. Собираем подсистемы отдельно для маятника и отдельно для тележки, и собираем все вместе. Результат на рисунке, модель в прикрепленных файлах.
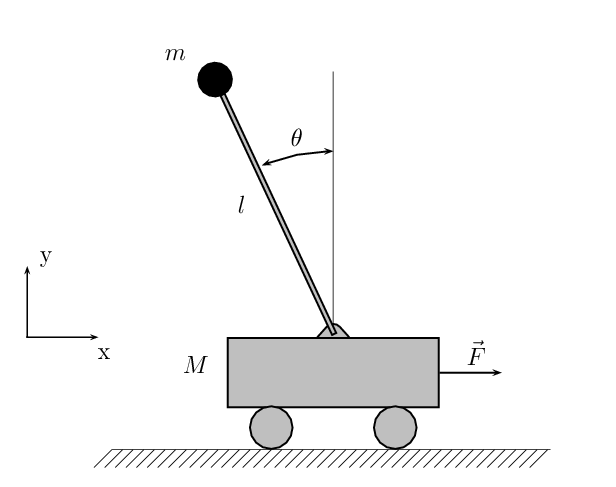
Классическим примером демонстрации возможностей теории управления является модель обратного маятника на тележке. В данной статье продемонстрируем решение классических проблем классическими методами, но в максимально тепличных условиях, когда всю рутинную работу за нас будут выполнять алгоритмы пакета MATLAB.
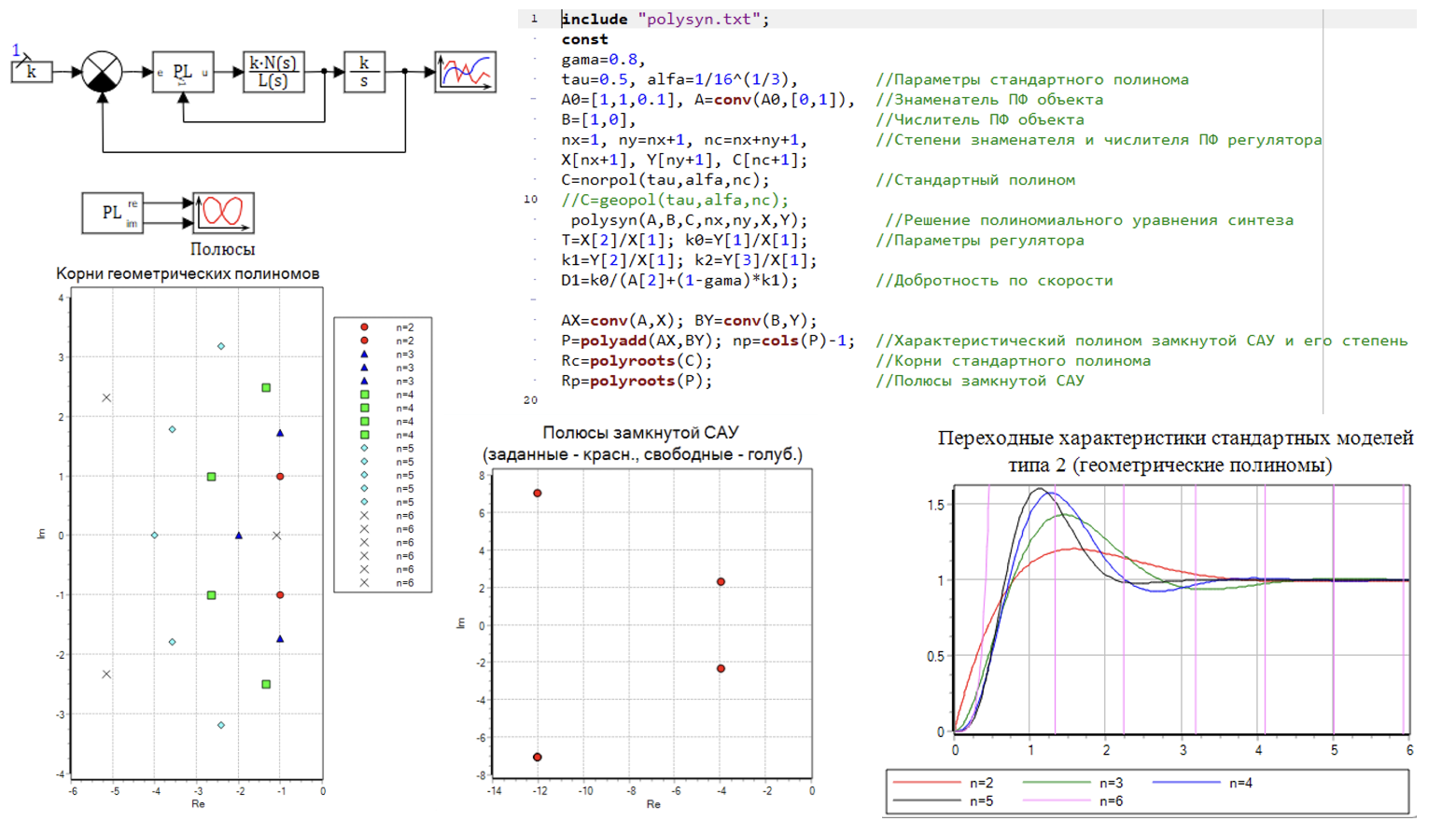
Леонид Маркович Скворцов. Широко известный в узких кругах математик, профессионально занимающийся математическими проблемами автоматического управления. Например, его авторские методы использованы в SimInTech. Данный текст, еще готовится к публикации. Но с разрешения автора, читатели Хабр будут первыми кто сможет оценить. Первая часть здесь... Вторая часть здесь...
Две предыдущие части были заполнены многоэтажными формулами в третей части разберем на примерах применение этих формул. Математику в жизнь!
Приведем примеры и покажем в видео как синтезировать регулятор для линейной модели двухроторного газотурбинного двигателя, работающего на базовом режиме малого газа, вместе с исполнительным механизмом. От теории к практике не приходя в сознание!

Леонид Маркович Скворцов. Широко известный в узких кругах математик, профессионально занимающийся математическими проблемами автоматического управления. Например, его авторские методы использованы в SimInTech. Данный текст, еще готовится к публикации. Но с разрешения автора, читатели Хабр будут первыми кто сможет оценить. Первая часть здесь...
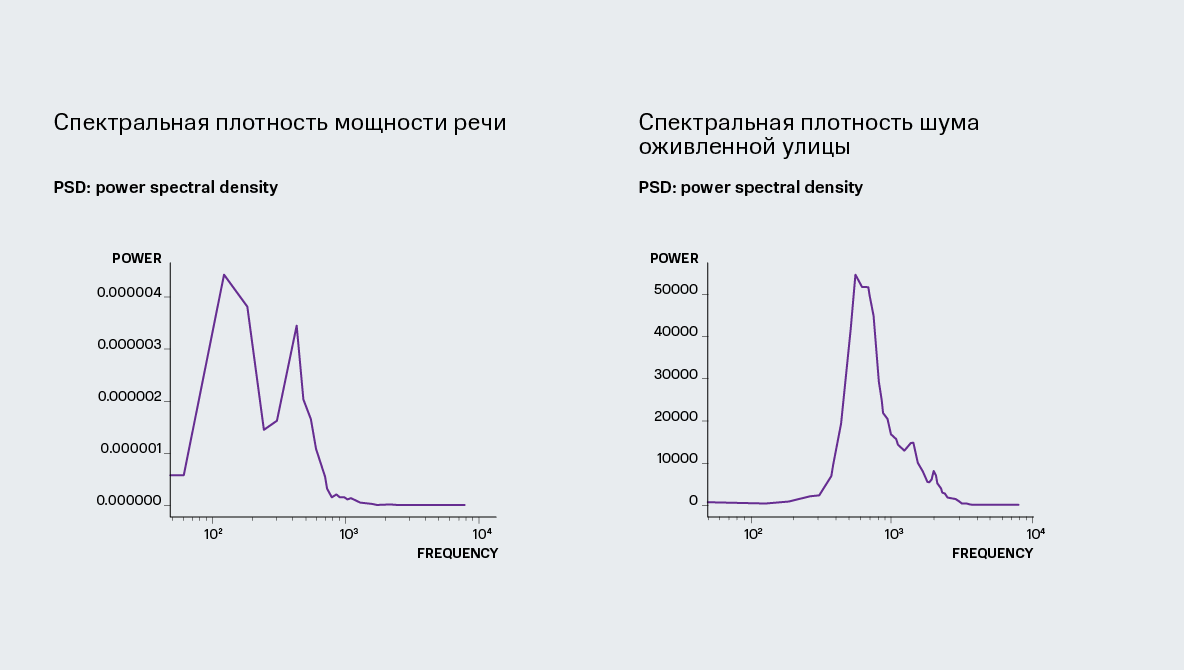
Обработка звука - это процесс исследования динамической/статической звуковой дорожки при помощи применения определенного набора линейных и нелинейных алгоритмов с целью получения необходимой информации.
Алгоритмы динамической обработки звука работают с потоковым аудио, когда статически обрабатывают уже готовую звуковую дорожку.
Данный процесс происходит с использованием компьютерных программ и зачастую сопровождается трудными техническими вычислениями, которые ложатся на вычислительные мощности компьютера или на отдельные его комплектующие части.
Процесс исследования и обработки звука так или иначе присутствует в разных сферах профессиональной деятельности, будь то голосовые помощники, встроенные в мобильные устройства или любые другие устройства, индустрия профессионального бизнес-сообщества для фиксирования необходимой информации или же специальные службы, использующие самые современные технологии для расследования преступлений.
Если мы говорим о задаче обработки звука, то чаще всего имеем в виду применение к звуковой дорожке определенного набора стандартных и собственных алгоритмов, которые позволяют получить определенный срез информации о дорожке или же получить новую трансформированную аудио дорожку.
Цель данной работы – исследовать алгоритмы удаления посторонних шумов из аудио дорожки.
Такое программное обеспечение будет полезно для автоматических субтитров во время онлайн-конференций, логирования бизнес-встреч, работы с глухонемыми и слабослышащими.
Пример решения системы дифференциальных уравнений (ДУ) в MATLAB адаптивным и не адаптивным методами.
В MATLAB встроено множество численных решателей с адаптивным шагом для решения жестких, нежестких и полностью неявных систем. С помощью Symbolic Math Toolbox можно сначала выводить системы ДУ, а затем тут же решать их численными методами.
Описание модели
Для примера решим систему ДУ, которая описывает систему из двух масс m1 и m2, которые жестко соединены невесомым стержнем длинной L.
Привет, Хабр! Представим, что перед нами такой сложный объект для управления, как электроэнергетическая система России. Чтобы рассматривать ее в виде единого целого, нужны высокоточные измерения из различных точек энергосистемы, зачастую географически удаленных друг от друга. Для решения этой задачи был создан стандарт IEEE C37.118. Он описывает так называемые синхрофазоры, или синхронизированные векторные измерения (СВИ).
В этой статье мы обсудим что такое СВИ и зачем они нужны, подробно разберем типы и форматы сообщений, рассмотрим, как передаются сообщения внутри стека TCP/IP, а также смоделируем пакеты С37.118 с помощью КПМ РИТМ и PMU Connection Tester.

Когда-то давно меня попросили разработать модель динамики полета АСП (авиационного средства поражения) в отечественном ПО, в среде SimInTech, причем разработать не с нуля, а тупо повторив уже созданную ранее модель в Матлабе (с Симулинком), и любезно выложенную в публичный доступ на гитхабе.
Я подумал - почему бы и нет, ведь в Симинтеке есть практически все требуемые блоки, а каких нет, я доработаю по образу и подобию. Без погружения в детали, в конце концов так оно и вышло. Но мне справедливо возразили - а чем докажешь, что твоя модель считает в точности так же, в динамике, как и исходная матлабовская модель?
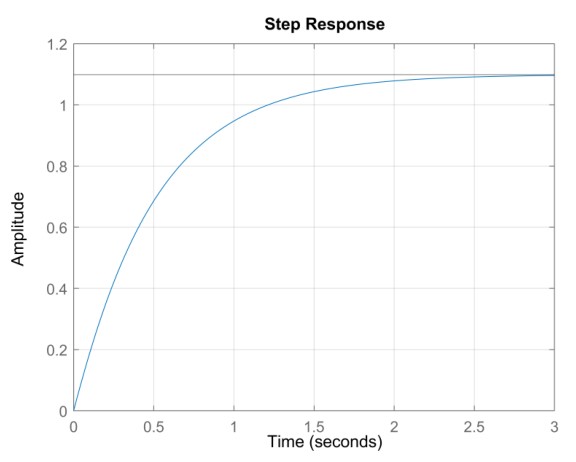
Частым заданием в различных курсах по теории автоматического управления является нахождение матрицы K для модального управления системой вида dx/dt = Ax+Bu y = Cx.
Такой тип задач легко решается в среде MATLAB.
Сперва наперво требуется задать нашу систему. Для примера возьмем типовую модель электродвигателя:
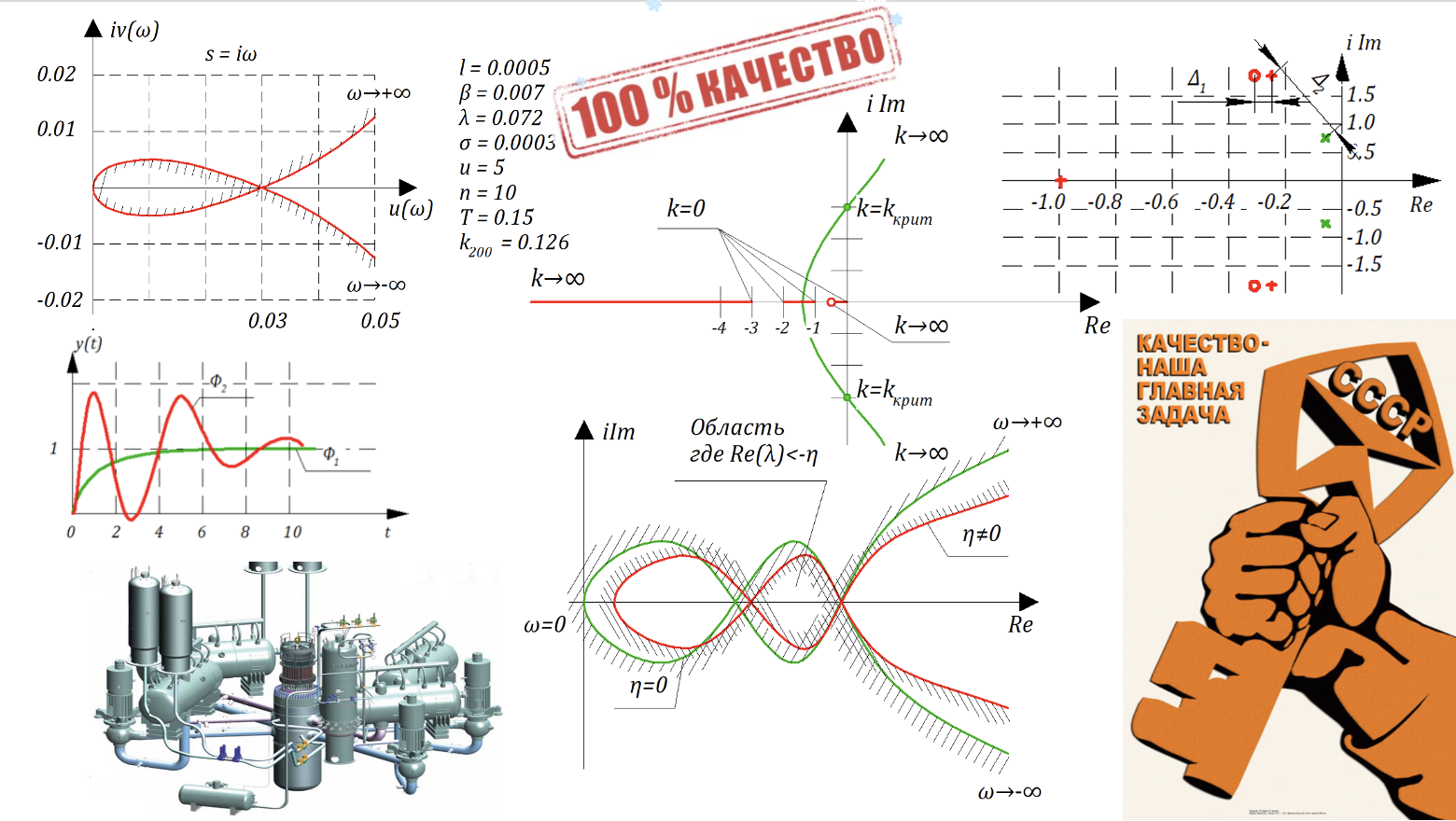
Продолжаем публикацию лекций Олега Степановича Козлова с кафедры Ядерные Энергетические Установки МГТУ им. Баумана. Вторая часть лекции про качество САР и модель реактора как бонус.
В предыдущих сериях:
1. Введение в теорию автоматического управления.
2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.
3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕГУЛИРОВАНИЯ. 3.1 Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2 Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3 Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4 Апериодическое звено 2-го порядка. 3.5 Колебательное звено. 3.6 Инерционно-дифференцирующее звено. 3.7 Форсирующее звено. 3.8 Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9 Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.
4. Структурные преобразования систем автоматического регулирования.
5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (САР).
6. Устойчивость систем автоматического регулирования. 6.1 Понятие об устойчивости САР. Теорема Ляпунова. 6.2 Необходимые условия устойчивости линейных и линеаризованных САР. 6.3 Алгебраический критерий устойчивости Гурвица. 6.4 Частотный критерий устойчивости Михайлова. 6.5 Критерий Найквиста.
7. Точность систем автоматического управления. Часть 1 и Часть 2
8. Качество переходного процесса. Часть 1
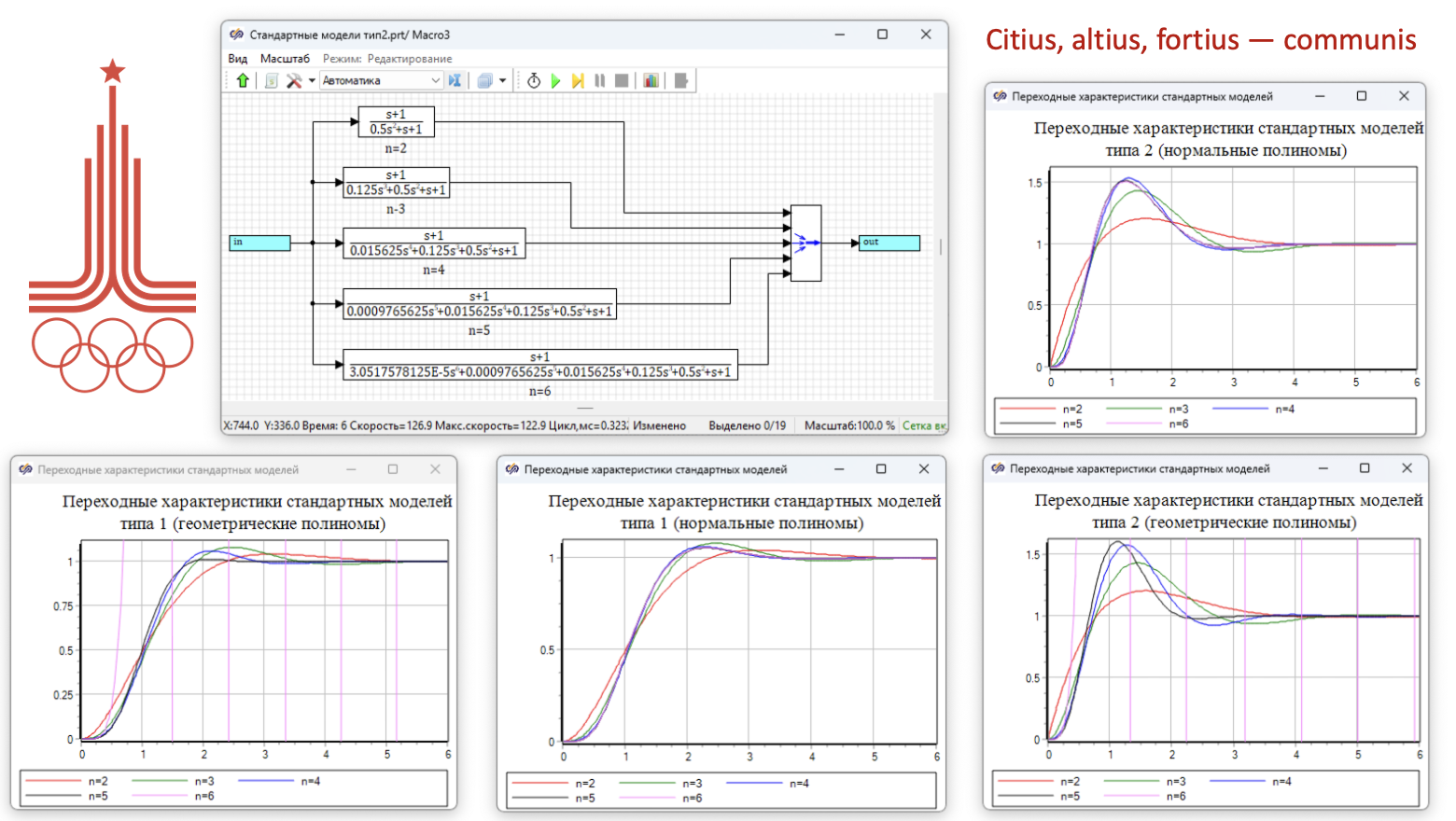
Ленонид Маркович Скворцов. Широко известный в узких кругах математик, профессионально занимающийся математическами проблемами автоматического управления. Например, его авторские методы использованы в SimInTech. Данный текст первая часть работы, которая еще готовится к публикации. Но с разрешения автора, читатели Хабр будут превыми кто сможет с ним ознакомится.
Все мы слышали, про преимущества советской математической школы над зарубежными математическими школами, но мало кто видел это приимущество в реальных задачах. В случае математических методов Леонида Марковича Скворцова, математика это не просто абстрактные формулы, а решение реальных прикладных задач, все можно увидеть пощупать и попробовать. В конце статьи видео-доказательство, практичесокй реализации преимуществ методов Леонида Марковича на практике.
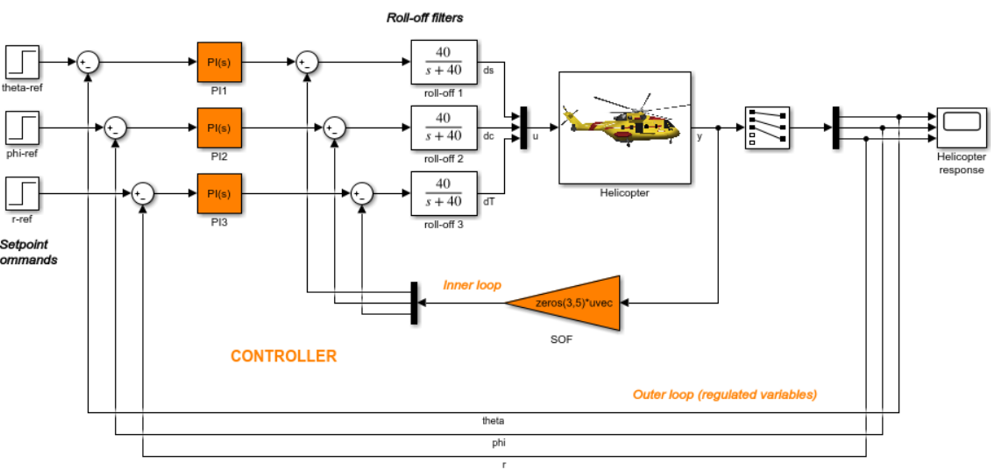
 . В этой работе рассматриваются особенности этого настройщика на примере построения двухконтурной системы управления.
. В этой работе рассматриваются особенности этого настройщика на примере построения двухконтурной системы управления. 
В предыдущих сериях:
1. Введение в теорию автоматического управления.
2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.
3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕГУЛИРОВАНИЯ. 3.1 Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2 Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3 Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4 Апериодическое звено 2-го порядка. 3.5 Колебательное звено. 3.6 Инерционно-дифференцирующее звено. 3.7 Форсирующее звено. 3.8 Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9 Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.
4. Структурные преобразования систем автоматического регулирования.
5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (САР).
6. Устойчивость систем автоматического регулирования. 6.1 Понятие об устойчивости САР. Теорема Ляпунова. 6.2 Необходимые условия устойчивости линейных и линеаризованных САР. 6.3 Алгебраический критерий устойчивости Гурвица. 6.4 Частотный критерий устойчивости Михайлова. 6.5 Критерий Найквиста.
7. Точность систем автоматического управления. Часть 1 и Часть 2
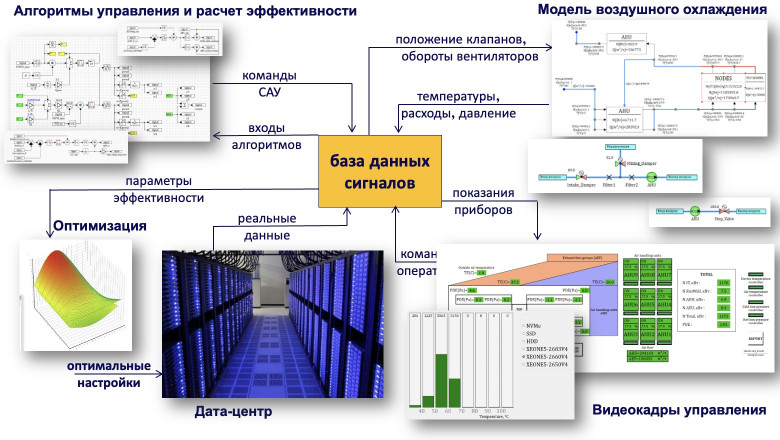
Все знают, что Россия — энергетическая сверхдержава, она же – «разорванная в клочья Обамой бензоколонка». Но не все знают, как это может отражаться в области развития математического моделирования. Расскажу одну жизненную историю.
Начну с далекого 2007 года. Довелось мне в те времена поработать на крупном заводе, который «эффективные менеджеры» как раз делили на несколько отдельных предприятий, каждое из которых крутилось, как могло. В том цеху, который и стал одним из таких предприятий, на токарных станках могла крутиться (и крутилась!) металлическая болванка размером с автобус. А в печку для нагрева металла можно было затолкать паровоз. Целиком. Когда я в первый раз увидел токарный станок, на котором крутится и обтачивается деталь размером с автобус, моему восторгу не было предела. Гордость за страну переполняла до состояния «в зобу дыханье сперло». А потом старожилы показали ту часть цеха, где стояли фундаменты таких же станков и пояснили:
- А вот тут были станки для точной обработки. Их продали китайцам по цене металлолома.
- А почему вот другие не продали?
- Потому, что у них точность обработки такая, что их только в металлолом можно сдать. Поэтому они здесь работают и крутятся как могут, и обтачивают валы турбин Siemiens.
Схема бизнеса был гениальна: Siemiens привозил на завод многотонные болванки, их неделями и месяцами обтачивали до состояния заготовок и увозили для чистовой обработки в Германию. Где уже выполняли чистовую доводку на точных и дорогих станках. Главные затраты при черновой обработке – это износ станков и инструмента, зарплата токаря и электроэнергия, необходимая для вращения тонн металла. Поскольку электроэнергия в РФ дешевле немецкой, недели обработки болванок с лихвой окупают транспортировку, а низкая точность обработки не требует дорогого обслуживания и мало чувствительна к износу еще советского оборудования. В итоге весь бизнес заключался в «перепродаже» дешевой электроэнергии из РФ в Германию, но в виде металлических обточенных болванок.
Возникла задача запускать графические приложения в полностью изолированной среде: как от Интернета, так и от файловой системы «хозяйской» ОС. В моём случае это был Matlab. Пишут, что в последних версиях он стал шибко «умным»: сам без спроса постоянно лезет в сеть и чем-то там постоянно обменивается со своими серверами. Однако использовать для поставленной задачи виртуальную гостевую машину / аппаратную виртуализацию (наподобие VirtualBox) — это, ИМХО, «too much». Docker подошел бы гораздо лучше, т.к. он использует то же ядро ОС и не требует эмуляции / виртуализации ввода-вывода, что существенно экономит ресурсы. Однако Docker «из коробки» не предназначен для запуска GUI-приложений. Что ж, попробуем это исправить и запустить таки Matlab внутри Docker-контейнера с полной поддержкой «иксов» и GUI.

В данной статье речь пойдет о создании счетчика расхода энергии батарейки.
Раньше я уже писал, что сталкивался с подобной задачей и тогда её удалось решить малой кровью. На "рынке" была микросхема кулоновского счетчика, которая подходила под потребление разрабатываемого устройства.
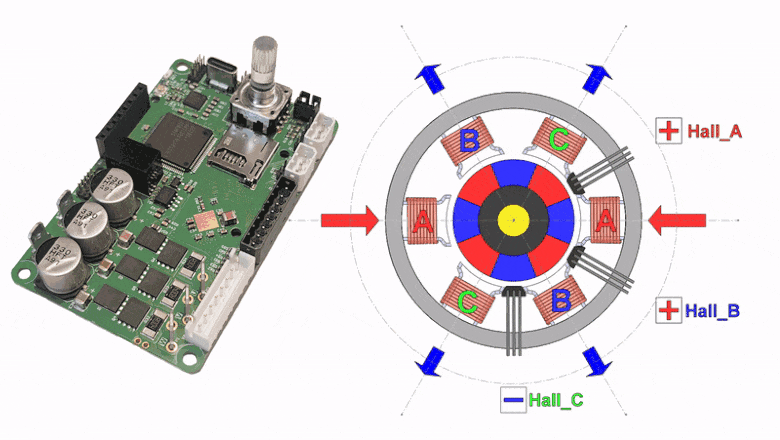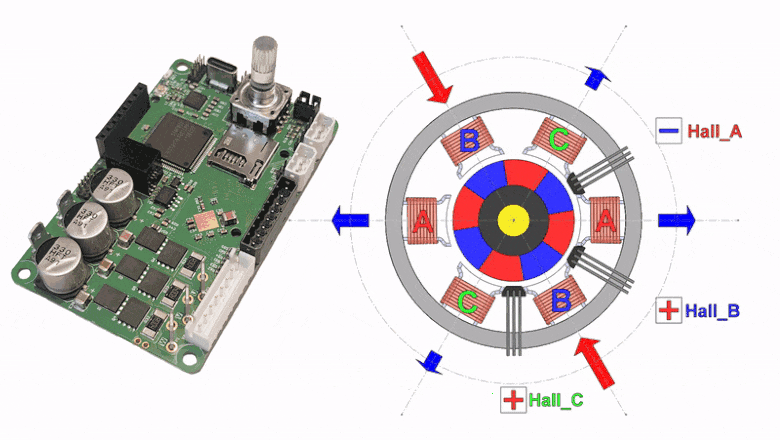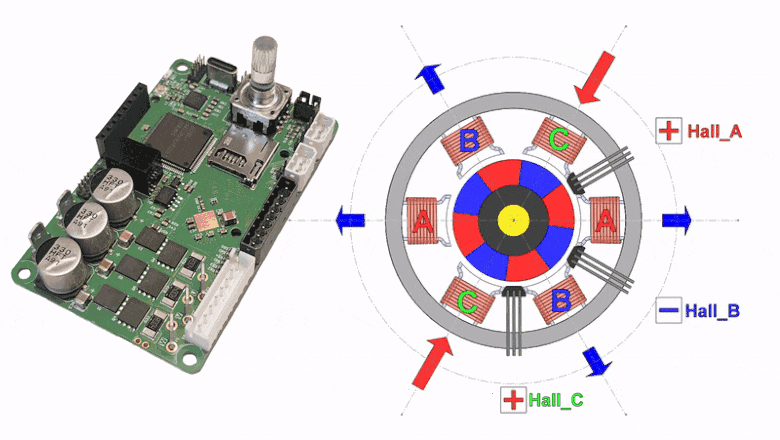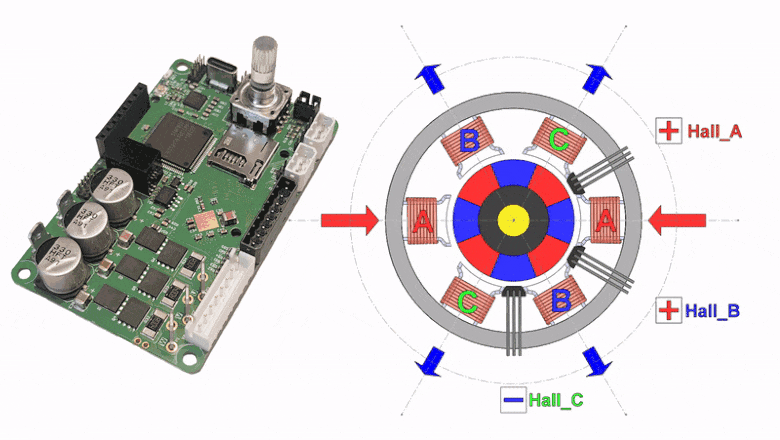
Здесь разрабатываем эталонную таблицу коммутации BLDC мотора на основе цифрового двойника и создаем алгоритм для автоматической генерации таблицы в сервоконтроллере MC50. Таблица коммутации используется для 6-шагового управления вращением ротора BLDC мотора с датчиками Холла. Хотя найти правильный способ коммутации несложно путём перебора (6! => 720 вариантов), но такой путь опасен неправильным выбором последовательности коммутаций, которые могут создать вращение, но крайне неэффективное и нестабильное.