Как же все таки они устроены? И кому это может быть полезно? Вам определенно с этим следует ознакомиться, если:
- Вы ими пользуетесь в своей торговле
- Вы планируете написать торгового робота
- Вы хотите реализовать торговую стратегию сами


Царица всех наук


 Поэзия — та же добыча радия.
Поэзия — та же добыча радия.
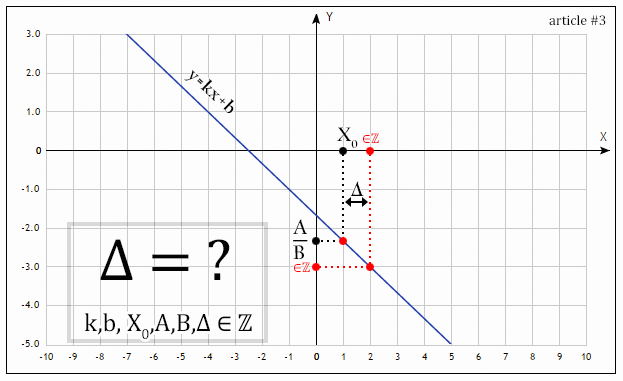
Что общего у нормального распределения, конечных автоматов, хеш-таблиц, произвольных предикатов, строк, выпуклых оболочек, афинных преобразований, файлов конфигураций и стилей CSS? А что объединяет целые числа, типы в Haskell, произвольные графы, альтернативные функторы, матрицы, регулярные выражения и статистические выборки? Наконец, можно ли как-то связать между собой булеву алгебру, электрические цепи, прямоугольные таблицы, теплоизоляцию труб или зданий и изображения на плоскости? На эти вопросы есть два важных ответа: 1) со всеми этими объектами работают программисты, 2) эти объекты имеют сходную алгебраическую структуру: первые являются моноидами, вторые — полукольцами, третьи — алгебрами де Моргана.
 Статистика приходит к нам на помощь при решении многих задач, например: когда нет возможности построить детерминированную модель, когда слишком много факторов или когда нам необходимо оценить правдоподобие построенной модели с учётом имеющихся данных. Отношение к статистике неоднозначное. Есть мнение, что существует три вида лжи: ложь, наглая ложь и статистика. С другой стороны, многие «пользователи» статистики слишком ей верят, не понимая до конца, как она работает: применяя, например, тест Стьюдента к любым данным без проверки их нормальности. Такая небрежность способна порождать серьёзные ошибки и превращать «поклонников» теста Стьюдента в ненавистников статистики. Попробуем поставить точки над i и разобраться, какие модели случайных величин должны использоваться для описания тех или иных явлений и какая между ними существует генетическая связь.
Статистика приходит к нам на помощь при решении многих задач, например: когда нет возможности построить детерминированную модель, когда слишком много факторов или когда нам необходимо оценить правдоподобие построенной модели с учётом имеющихся данных. Отношение к статистике неоднозначное. Есть мнение, что существует три вида лжи: ложь, наглая ложь и статистика. С другой стороны, многие «пользователи» статистики слишком ей верят, не понимая до конца, как она работает: применяя, например, тест Стьюдента к любым данным без проверки их нормальности. Такая небрежность способна порождать серьёзные ошибки и превращать «поклонников» теста Стьюдента в ненавистников статистики. Попробуем поставить точки над i и разобраться, какие модели случайных величин должны использоваться для описания тех или иных явлений и какая между ними существует генетическая связь.Это седьмая статья из цикла «Теория категорий для программистов». Предыдущие статьи уже публиковались на Хабре:
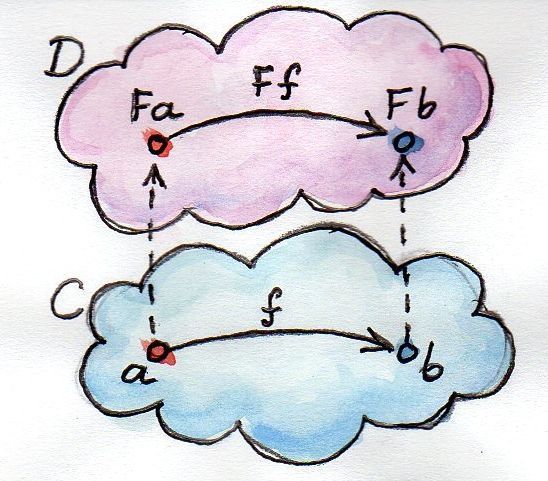
За понятием функтора стоит очень простая, но мощная идея (как бы заезжено это ни прозвучало). Просто теория категорий полна простых и мощных идей. Функтор есть отображение между категориями. Пусть даны две категории C и D, а функтор F отображает объекты из C в объекты из D — это функция над объектами. Если a — это объект из C, то будем обозначать его образ из D как F a (без скобок). Но ведь категория — это не только объекты, но еще и соединяющие их морфизмы. Функтор также отображает и морфизмы — это функция над морфизмами. Но морфизмы отображаются не как попало, а так, чтобы сохранять связи. А именно, если морфизм f из C связывает объект a с объектом b,
f :: a -> bто образ f в D, F f, связывает образ a с образом b:
F f :: F a -> F b(Надеемся, что такая смесь математических обозначений и синтаксиса Haskell понятна читателю. Мы не будем писать скобки, применяя функторы к объектам или морфизмам.)

Тензор — математический объект, не изменяющийся при изменении системы координат, представленный набором >своих компонент и правилом преобразования компонент при смене базиса.



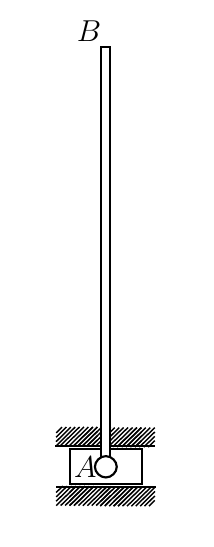
Тонкий однородный стержень массы m = 2 кг, длины AB = 2l = 1 м в точке A шарнирно прикреплен к невесомому ползуну, перемещающемуся в горизонтальных шероховатых направляющих. В начальный момент времени стержень расположен вертикально, затем его отклоняют от вертикали на ничтожно малый угол и отпускают без начальной скорости. Необходимо составить уравнения движения данной механической системы и найти закон её движения. Коэффициент трения между ползуном и направляющими равен f = 0,1.

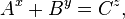
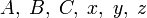 — натуральные и
— натуральные и 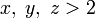 , то
, то 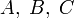 имеют общий простой делитель.
имеют общий простой делитель.