Неожиданно статья про мой опыт автоматизации однокомнатной квартиры площадью 41 кв. м. в новостройке, опубликованная две недели назад, стала популярна и на 10 марта её добавил в закладки 781 человек, просмотрели 123 921 раз и Хабр даже запилил рекламный блок в разделе «Рекомендуем» с пометкой «Интересно».


1500 метров проложенных кабелей после окончания ремонта не видны. На фото спальня

Перед вами продолжение истории, где я отвечу на комментарии, приведу фотографии квартиры с мебелью, получившиеся электрические щиты, а также расскажу о тех сложностях, с которыми я столкнулся после того, как перешёл c openHAB в другую систему домашней автоматизации — Home Assistant.

Три года назад стал претворять свою давнюю мечту в реальность — максимальная домашняя автоматизация квартиры, купленной в новостройке с нуля. При этом «отделку от застройщика» пришлось принести в жертву умному дому и полностью переделать, а вся электрика, не связанная с автоматикой приехала с известного китайского сайта. Паяльник не потребовался, но знающих мастеров, электриков и плотников пришлось искать долго.


Панель управления квартирой в феврале 2020 года (Home Assistant)

В этой статье расскажу о выборе технологий умного дома, используемых в квартире, а также приведу мои схемы разводки, фотографии всего что было сделано, получившиеся электрические щиты и конфигурации всех устройств, дам ссылку на гитхаб.


Строительство нашего дома в процессе — ноябрь 2016 года

Перевод статьи подготовлен специально для студентов курса «Разработчик Python».

---

Когда вы пишете на низкоуровневом языке, таком как С, вы беспокоитесь о выборе правильного типа данных и спецификаторах для ваших целых чисел, на каждом шаге анализируете достаточно ли будет использовать просто int или нужно добавить long или даже long double. Однако при написании кода на Python вам не нужно беспокоиться об этих «незначительных» вещах, потому что Python может работать с числами типа integer любого размера.

---

Эта статья — перевод статьи Томаса Нильда How It Feels to Learn Data Science in 2019

---

Видение (случайного) леса через деревья (решений)

Thomas Nield Follow Feb 4
Время чтения: 16 минут

Мне давно было интересно, как сжимаются данные, в том числе в Zip-файлах. Однажды я решил удовлетворить своё любопытство: узнать, как работает сжатие, и написать собственную Zip-программу. Реализация превратилась в захватывающее упражнение в программировании. Получаешь огромное удовольствие от создания отлаженной машины, которая берёт данные, перекладывает их биты в более эффективное представление, а затем собирает обратно. Надеюсь, вам тоже будет интересно об этом читать.

В статье очень подробно объясняется, как работают Zip-файлы и схема сжатия: LZ77-сжатие, алгоритм Хаффмана, алгоритм Deflate и прочее. Вы узнаете историю развития технологии и посмотрите довольно эффективные примеры реализации, написанные с нуля на С. Исходный код лежит тут: hwzip-1.0.zip.

Статья посвящена языку ассемблер с учетом актуальных реалий. Представлены преимущества и отличия от ЯВУ, произведено небольшое сравнение компиляторов, скрупулёзно собрано значительное количество лучшей тематической литературы.

Лето — пора путешествий и заслуженного отдыха.  Каким бы ни было путешествие и куда бы вы ни направлялись, наверняка, это будет длинная дорога (авиаперелет или поезд), или же среднего качества связь, если мы говорим об удаленных от благ цивилизации местах.

Обычно запасливые люди берут с собой в путешествие кучу фильмов и сериалов, чтобы было чем заткнуть уши в транспорте и слушать голоса любимых персонажей.

Мы приготовили для вас небольшую подборку сериалов, так или иначе связанных с ИT. А натолкнула нас на идею этого поста многолетняя дружба ЛАНИТ с Международным фестивалем документального кино "ДОКЕР", где, кстати, в том числе с нашей помощью традиционной стала номинация для фильмов о возможностях информационных технологий «Let IT Doк!».

Кадр из сериала «Mr. Robot» (eps3.1_undo.gz)

Веб-скрапинг — это метод сбора данных с веб-сайтов. Этот термин обычно используется в применении к автоматизированному сбору данных. Сегодня мы поговорим о том, как собирать данные с сайтов анонимно. Причина, по которой некто может захотеть анонимности в деле веб-скрапинга, заключается в том, что многие веб-серверы применяют определённые правила к подключениям с IP-адресов, с которых за некий отрезок времени выполнено какое-то количество запросов. Здесь мы будем пользоваться следующими инструментами:

• Puppeteer — для доступа к веб-страницам.
• Cheerio — для парсинга HTML-кода.
• Tor — для выполнения каждого запроса с различного IP-адреса.

Надо отметить, что правовые аспекты веб-скрапинга — вопрос непростой и часто неясный. Поэтому уважайте «Условия использования» тех страниц, данные которых вы собираете. Вот хороший материал на эту тему.

Доброго времени суток, Хабрахабр! Данный материал является продолжением первой части, в которой освещены инструменты и возможности разработки продукта на облачной платформе. Примером является актуальное мобильное расширение доступа к расписанию пар в университете — Telegram-bot.

Уделив время первой публикации, вы можете ознакомиться не только с первоначальным развертыванием и необходимыми ресурсами, но и с обзором приложения от автора. Информация ниже сконцентрирована в большей степени на описании технической стороны и в меньшей на выводах по итогам на текущий момент.

Доброго времени суток, Хабрахабр! Целью статьи является рассказать начинающим программистам о возможности не только разработать что-то интересное на основе несложных инструментов, но и разместить проект в общий доступ, а при усердных стараниях увидеть, что не только автор может оценить потраченные усилия.

Ближе к делу — мой первый пет-проект, решающий проблему доступа к расписанию университета на мобильных устройствах через Telegram, с аудиторией более, чем сто пятьдесят уникальных посетителей в сутки. Несмотря на то, что цифра не является заоблачной, это совсем неплохой результат, выступающий последующей долговременной средой настоящей боевой разработки, учитывая все возможные особенности, и сопровождения продукта длительный период, что бесспорно полезно и ценно для каждого разработчика.

Одна простая клавиша Ctrl может значительно упростить работу в Visual Studio. Помимо типичных комбинаций, которые нам очень хорошо знакомы, существует также и большое количество других, менее известных, но от этого и более ценных.

Далее список того, что можно делать с клавишей Ctrl.

В рамках предыдущего моего проекта, «Видеофон из Raspberry Pi», мне довелось для настройки оборудования и решения проблемы, воспользоваться утилитой Iperf. Программа давно известная в кругу специалистов, работающих с локальными сетями.

Утилита позволяет генерировать трафик для анализа пропускной способности сети.

С ее помощью, довольно просто измерить максимальную пропускную способность сети между двумя устройствами (сервером и клиентом) и провести нагрузочное тестирование канала связи.
Думаю, в связи с увеличением домашних сетевых устройств, она будет довольно востребована, как для поиска и анализа неисправностей (сбоев) в работе, так и для оптимального размещения WiFi оборудования.

В моем примере, программа устанавливалась на Raspberry Pi с установленной системой домашней автоматизации MajorDoMo — базовый образ, и на устройства, работающие под ОС Windows (ноутбук), Android (смартфон, ТВ, медиаплеер).

Под катом немного про установку и тестирование, а также небольшой пример интеграции в систему домашней автоматизации MajorDoMo.

Статья о том, как мне удалось запустить VPN-сервер за NAT'ом домашнего провайдера (без белого IP-адреса). Сразу оговорюсь: что работоспособность данной реализация напрямую зависит от типа NAT используемого Вашим провайдером, а также роутером.
Итак, возникла у меня необходимость подключаться со своего Android-смартфона к домашнему компьютеру, оба девайса подключены к Интернету через провайдерские NAT'ы, плюсом компьютер подключен через домашний роутер, который тоже NAT'ил соединения.
Классическая схема с использованием арендованного VPS/VDS с белым IP-адресом, а также аренда белого IP-адреса у провайдера не рассматривалась по нескольким причинам.

Привет!

Калькулятор у нас почему-то ассоциируется с чем-то, что должен написать каждый новичок. Возможно потому, что исторически компьютеры с той целью и создавались, чтобы считать. Но мы будем писать непростой калькулятор, не sympy конечно, но чтобы умел базовые алгебраические операции, типа дифференциирования, симплификации, а также фичи типа компиляции для ускорения вычислений.


Берем оставшиеся с нового года печеньки, и погнали!

Статья состоит из двух частей:

1. Краткое описание некоторых архитектур сетей по обнаружению объектов на изображении и сегментации изображений с самыми понятными для меня ссылками на ресурсы. Старался выбирать видео пояснения и желательно на русском языке.
2. Вторая часть состоит в попытке осознать направление развития архитектур нейронных сетей. И технологий на их основе.

Рисунок 1 – Понимать архитектуры нейросетей непросто

Все началось с того, что сделал два демонстрационных приложения по классификации и обнаружению объектов на телефоне Android:

• Back-end demo, когда данные обрабатываются на сервере и передаются на телефон. Классификация изображений (image classification) трех типов медведей: бурого, черного и плюшевого.
• Front-end demo, когда данные обрабатываются на самом телефоне. Обнаружение объектов (object detection) трех типов: фундук, инжир и финик.

Я бы хотел получить такое письмо три года назад, когда только начинал изучать Data Science (DS). Чтобы там были необходимые ссылки на полезные материалы. Статья не претендует на полноту охвата необъятной области DS. Однако для начинающего специалиста будет полезна.

Клеточный автомат — это система, состоящая из клеток с численными значениями в сетке, а также из правил, определяющих поведение этих клеток. Многократно применяя правило к каждой клетке сетки параллельно с визуализацией сетки, часто можно получить эффект некоего эволюционирующего организма со сложным и замысловатым поведением, даже если правила относительно просты.

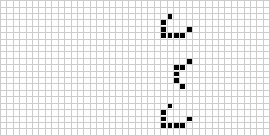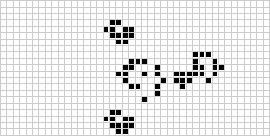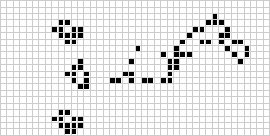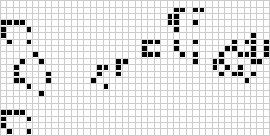
Клеточные автоматы имеют различные формы, виды и размерности. Наверно, самым знаменитым клеточным автоматом является конвеевская игра «Жизнь» (Conway's Game of Life, GOL). Она состоит из двухмерной сетки, в которой каждая клетка содержит двоичное значение (живая или мёртвая). Сопутствующие правила на основании состояния соседних клеток определяют, должна ли клетка быть мёртвой или живой. Правила гласят, что живая клетка умирает от одиночества, если вокруг неё меньше 2 живых клеток. Если живы больше трёх соседних клеток, она погибает от перенаселённости. Другими словами, клетка «выживает», если вокруг неё ровно 2 или 3 живых соседних клеток. Чтобы мёртвая клетка ожила, у неё должно быть ровно 3 живых соседних клеток, в противном случае она остаётся мёртвой. Пример автомата GoL, итеративно проходящий несколько состояний, показан ниже.


Ещё один знаменитый вариант клеточного автомата одномерен; он называется элементарным клеточным автоматом (Elementary Cellular Automaton, ECA). Именно его мы реализуем в этом посте.

Написано очень много статей, посвящённых интересным возможностям Python. В них идёт речь о распаковке списков и кортежей в переменные, о частичном применении функций, о работе с итерируемыми объектами. Но в Python есть гораздо больше всего интересного. Автор статьи, перевод которой мы сегодня публикуем, говорит, что хочет рассказать о некоторых возможностях Python, которыми он пользуется. При этом описания этих возможностей, подобного тому, которое приведено здесь, ему пока не встречалось. Возможно, что и вы о них тоже ещё нигде не читали.

В рамках открытого курса по машинному обучению мы продолжаем общаться с заметными представителями этой области. Нашими первыми собеседниками были Александр Дьяконов, Константин Воронцов и Евгений Соколов, см. видео в YouTube-канале курса. В этот раз мы пообщались с Дмитрием Ветровым.

Всем привет!

Вот мы постепенно и дошли до продвинутых методов машинного обучения. Сегодня обсудим, как вообще подступиться к обучению модели, если данных гигабайты или десятки гигабайт. Обсудим приемы, позволяющие это делать: стохастический градиентный спуск (SGD) и хэширование признаков, посмотрим на примеры применения библиотеки Vowpal Wabbit.

UPD 01.2022: С февраля 2022 г. ML-курс ODS на русском возрождается под руководством Петра Ермакова couatl. Для русскоязычной аудитории это предпочтительный вариант (c этими статьями на Хабре – в подкрепление), англоговорящим рекомендуется mlcourse.ai в режиме самостоятельного прохождения.

Видеозапись лекции по мотивам этой статьи в рамках второго запуска открытого курса (сентябрь-ноябрь 2017).