Теореме Гёделя о неполноте, одной из самых известных теорем математической логики, повезло и не повезло одновременно. В этом она похожа на специальную теорию относительности Эйнштейна. С одной стороны, почти все о них что-то слышали. С другой — в народной интерпретации теория Эйнштейна, как известно, «говорит, что всё в мире относительно». А теорема Гёделя о неполноте (далее просто ТГН), в примерно столь же вольной фолк-формулировке, «доказывает, что есть вещи, непостижимые для человеческого разума». И вот одни пытаются приспособить её в качестве аргумента против материализма, а другие, напротив, доказывают с её помощью, что бога нет. Забавно не только то, что обе стороны не могут оказаться правыми одновременно, но и то, что ни те, ни другие не удосуживаются разобраться, что же, собственно, эта теорема утверждает.
Итак, что же? Ниже я попытаюсь «на пальцах» рассказать об этом. Изложение моё будет, разумеется нестрогим и интуитивным, но я попрошу математиков не судить меня строго. Возможно, что для нематематиков (к которым, вообще-то, отношусь и я), в рассказанном ниже будет что-то новое и полезное.
Математическая логика — наука действительно довольно сложная, а главное — не очень привычная. Она требует аккуратных и строгих манёвров, при которых важно не перепутать реально доказанное с тем, что «и так понятно». Тем не менее, я надеюсь, что для понимания следующего ниже «наброска доказательства ТГН» читателю понадобится только знание школьной математики/информатики, навыки логического мышления и 15-20 минут времени.






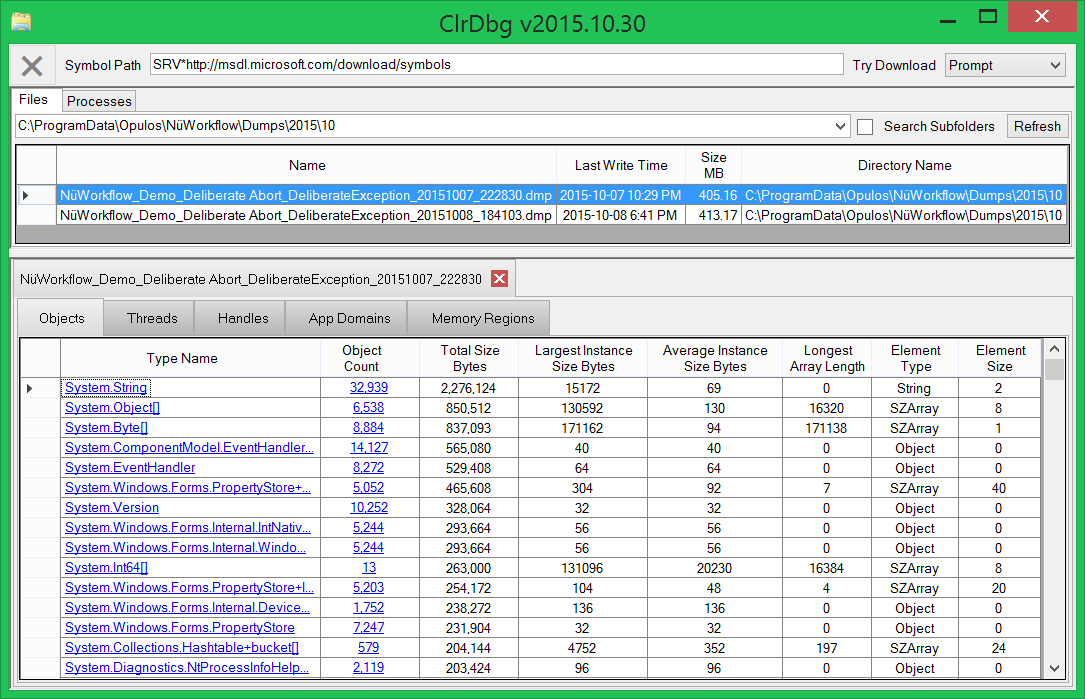
 Не всегда разрабатываемое решение работает с приемлемой производительностью. Особенно для заказчика. И если предложение докупить памяти и поднять системные требования не срабатывает (у меня ни разу не получалось), приходится браться за оптимизацию. И для этого у нас есть не только StopWatch: об инструментах, которые позволяют понять, где искать, куда лезть в первую очередь, каких результатов ждать, работая над перфомансом приложения, поговорили с прекрасной девушкой, отличным специалистом и докладчиком конференции DotNext 2016 Moscow —
Не всегда разрабатываемое решение работает с приемлемой производительностью. Особенно для заказчика. И если предложение докупить памяти и поднять системные требования не срабатывает (у меня ни разу не получалось), приходится браться за оптимизацию. И для этого у нас есть не только StopWatch: об инструментах, которые позволяют понять, где искать, куда лезть в первую очередь, каких результатов ждать, работая над перфомансом приложения, поговорили с прекрасной девушкой, отличным специалистом и докладчиком конференции DotNext 2016 Moscow — 

