Вступление
В этой небольшой статье я расскажу о теории категорий в контексте системы типов языка Haskell. Никакой зауми, никаких уловок – постараюсь объяснять всё наглядно. Я хочу показать тесную связь языка программирования с математикой, чтобы спровоцировать у читателя осознание одного, через другое и наоборот.
Не хотелось бы повторять перевод на эту тему, который уже был на хабре:
Монады с точки зрения теории категорий, но для целостности статьи, я всё же буду давать основные определения. При этом, в отличие от той статьи, я не хочу делать основной упор на математику.
Эта статья во многом повторяет (в том числе заимствует иллюстрации) раздел из английской
Haskell Wikibook, но тем не менее не является непосредственным переводом.
Что такое категория?
Примеры
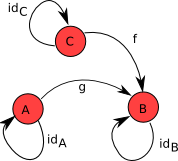
Для наглядности рассмотрим сначала пару картинок изображающих простые категории. На них есть красные кружочки и стрелки:
Красные кружочки изображают «объекты», а стрелки – «морфизмы».
Я хочу привести один наглядный пример из реальной жизни, который даст какое-то интуитивное представление о природе объектов и морфизмов:
Можно считать города «объектами», а перемещения между городами – «морфизмами». Например, можно представить себе карту авиарейсов (как-то не нашёл я удачную картинку) или карту железных дорог – они будут похожи на картинки выше, только сложнее. Следует обратить внимание на два момента, которые кажутся в реальности само собой разумеющимися, но для дальнейшего имеют важное значение:
- Бывает, что из одного города в другой никак не попасть поездом или самолётом – между этими городами нет морфизмов.
- Если мы перемещаемся в пределах одного и того же города, то это тоже морфизм – мы как бы путешествуем из города в него же.
- Если из Санкт-Петербурга есть поезд до Москвы, а из Москвы есть авиарейс в Амстердам, то мы можем купить билет на поезд и билет на самолёт, “скомбинировать” их и таким образом попасть из Санкт-Петербурга в Амстердам – то есть можно на нашей карте нарисовать стрелку от Санкт-Петербурга до Амстердама изображающую этот скомбинированный морфизм.
Надеюсь, с этим примером всё понятно. А теперь немного формализма для чёткости.